- Erstellt von Ann-Kristin Kreutzmann, zuletzt aktualisiert von Anonym vor etwa 4 Stunden Lesedauer: 17 Minute(n)
Datensätze können sehr unübersichtlich sein. Die deskriptive („beschreibende“) Statistik stellt ein Bündel an Verfahren, Grafiken und Parametern bereit, welche es ermöglichen, die Informationen soweit zu verdichten, dass man sich schnell einen Eindruck über die Daten verschaffen kann. Eine deskriptive Auswertung sollte am Anfang jeder statistischen Analyse stehen. Sie vermittelt dem/der Forscher/-in ein Gefühl für die Daten und hilft ggf., vorhandene Fehler und unplausible Werte (z.B. Ausreißer/ Outlier) zu entdecken. Wichtig hierfür ist die Kenntnis über das Skalenniveau der Daten, die untersucht werden sollen, da die Wahl des Mittels zur Beschreibung eines Datensatzes von diesem abhängt.
Beginnt man mit der Auswertung einer empirischen Studie so ist es sinnvoll, sich zuerst einen Überblick über den vorliegenden Datensatz zu verschaffen, bevor die angestrebten Auswertungsmethoden angewandt werden. Hierbei geben Lage- und Skalenparameter erste Informationen zu dem Datensatz. Die Visualisierung der Daten ist für das bessere Verständnis des Datensatzes erforderlich. Durch diese kann ein Eindruck von der Verteilung der Merkmale oder dem Zusammenhang zwischen unterschiedlichen Merkmalen gewonnen werden.
Inhaltsverzeichnis
fu:stat bietet regelmäßig Schulungen für Hochschulangehörige sowie für Unternehmen und weitere Institutionen an. Die Inhalte reichen von Statistikgrundlagen (Deskriptive, Testen, Schätzen, lineare Regression) bis zu Methoden für Big Data. Es werden außerdem Kurse zu verschiedenen Software-Paketen gegeben.
Häufigkeits- und Kontingenztabellen
Häufigkeitstabellen
Das einfachste Mittel zur Darstellung der Verteilung von Ausprägungen eines Merkmals ist die Häufigkeitstabelle. Das Aufstellen einer Häufigkeitstabelle ist insbesondere für diskrete Merkmale mit einer überschaubaren Anzahl an Ausprägungen sinnvoll. Das Beispiel zeigt eine Häufigkeitstabelle für eine fiktive Umfrage zur Zufriedenheit mit einem bestimmten Produkt (1 bedeutet sehr unzufrieden, 5 sehr zufrieden):
Merkmalsausprägung | absolute Häufigkeit | relative Häufigkeit | kumulierte rel. Häufigkeit |
|---|---|---|---|
| 1 | 1 | 0,05 | 0,05 |
| 2 | 2 | 0,10 | 0,15 |
| 3 | 4 | 0,20 | 0,35 |
| 4 | 8 | 0,40 | 0,75 |
| 5 | 5 | 0,25 | 1,00 |
Häufigkeitstabellen
In dieser Häufigkeitstabelle zu der Zufriedenheit der Konsumenten mit einem fiktiven Produkt sind die absoluten, relativen und kumulierten relativen Häufigkeiten für die jeweilige Merkmalsausprägung (hier: Zufriedenheit mit dem Produkt) dargestellt.
Die erste Spalte der Tabelle enthält die Ausprägungen, die zweite Spalte („absolute Häufigkeit“) zählt, wie oft die jeweilige Ausprägung im Datensatz vorkommt. Die „relative Häufigkeit“ gibt den Anteil des Vorkommens der Ausprägung an. Dieser berechnet sich aus der absoluten Häufigkeit dividiert durch die Gesamtanzahl der Untersuchungseinheiten. Die Anzahl der Untersuchungseinheiten wird bei Teilerhebungen auch als Stichprobenumfang (Symbol: n) bezeichnet und entspricht der Summe der absoluten Häufigkeiten. Die Summe der relativen Häufigkeiten ergibt 1 (100%). Die letzte Spalte enthält die sog. „kumulierte relative Häufigkeit“, also die Summe der relativen Häufigkeiten bis zur aktuellen Zeile. Diese Spalte lässt sich nur bei Variablen mit ordinalem oder metrischem Messniveau sinnvoll interpretieren.
Beispiele:
• absolute Häufigkeit der Zufriedenheit = 5: 5 (fünf Personen sind mit dem Produkt sehr zufrieden)
• relative Häufigkeit der Zufriedenheit = 2: 0,1 (10% = 1/10 der Personen sind mit dem Produkt tendenziell unzufrieden)
• kumulierte relative Häufigkeit der Zufriedenheit = 2: 0,15 (15% der befragten Personen sind mit dem Produkt unzufrieden oder tendenziell unzufrieden)
Bei Variablen mit sehr vielen Ausprägungen (oft bei metrischem Messniveau) werden Häufigkeitstabellen zu unübersichtlich, weil sie für jede Ausprägung eine Zeile enthalten. Abhilfe schafft die Klassierung des Merkmals. Bei der Klassierung werden statt einzelnen Merkmalsausprägungen bestimmte Bereiche betrachtet. Ein Beispiel könnte folgende Klassierung der Variable Größe aus dem ALLBUS Datensatz sein:
- Klasse: 140 cm bis einschließlich 145 cm
- Klasse: über 145 cm bis einschließlich 150 cm
- Klasse: über 150 cm bis einschließlich 155 cm usw.
Statt der einzelnen Ausprägungen werden nun die Klassen verwendet, für die dann absolute, relative und kumulierte relative Häufigkeit in einer Häufigkeitstabelle zusammengeführt werden können.
Kontingenztabellen
Die Häufigkeitstabelle stellt die Verteilung eines Merkmals dar. Nicht selten liegt das Interesse aber darüber hinaus bei der Suche nach Zusammenhängen zwischen zwei oder mehr Merkmalen. Für diesen Zweck eignen sich Kontingenztabellen (auch „Kreuztabellen“ genannt), die simultan die Verteilung von zwei (oder auch mehr) diskreten Merkmalen darstellen. Die Kontingenztabelle enthält in der Regel absolute oder relative Häufigkeiten. In bestimmten Situationen hilfreich sind auch Kontingenztabellen mit sog. bedingten relativen Häufigkeiten in den Zeilen oder Spalten.
Mehr Informationen zu Kontingenztabellen finden sich im Abschnitt Standardauswertungen.
Lage- und Skalenparameter
Lage- und Skalenparameter sind bei der ersten Analyse von Daten äußerst nützlich, da Informationen, die zu einem Merkmal im Datensatz vorliegen, auf einen Wert verdichtet werden können.
Modus
Als Lageparameter für nominal-skalierte Variablen wird in der Regel der Modus empfohlen, denn sowohl arithmetisches Mittel, als auch Median können nicht verwendet werden. Der Modus entspricht immer der Merkmalsausprägung, die am häufigsten realisiert wurde. Bei einer Umfrage nach den Geburtsmonaten in einer Klasse beispielsweise, stellt der Monat den Modus dar, in dem die meisten Schüler Geburtstag haben.
Hat das untersuchte Merkmal mindestens ein ordinales Skalenniveau, kann die zugehörige Häufigkeitsverteilung auch bi- oder sogar multimodal sein. In diesem Fall ist der Modus nicht mehr eindeutig.
Verwendet man klassierte Daten, gibt man die modale Klasse an und weißt als Modus die Klassenmitte der modalen Klasse aus.
Arithmetisches Mittel
Das arithmetische Mittel wird umgangssprachlich als Durchschnitt bezeichnet. Es berechnet sich aus der Summe aller beobachteten Merkmalsausprägungen x1, x2, . . . , xn dividiert durch den Stichprobenumfang n:
$$\bar{x}_{arithm.}=\frac{1}{n}\sum_{i=1}^{n}x_{i}$$
Somit stellt das arithmetische Mittel einen Spezialfall gewichteter Mittel dar, da jede Merkmalsausprägung mit der Konstanten \(\frac{1}{n}\) gleichgewichtet wird. Das arithmetische Mittel lässt sich als „Schwerpunkt der Daten“ interpretieren, da gilt: \(\sum_{i=1}^{n}(x_i - \bar{x}) = 0\)
Vor-/Nachteile des arithmetischen Mittels:
+ bekanntester Lageparameter
+ leicht und anschaulich zu interpretieren
- wird stark durch extreme Werte in den Daten beeinflusst (nicht robust) -> mögliche Abhilfe: getrimmtes arithmetisches Mittel
- nur für Merkmale mit metrischem Messniveau geeignet (die Abstände zwischen den Werten müssen interpretierbar sein)
Median
Der Median wird in statistischen Untersuchungen immer häufiger anstelle des arithmetischen Mittels oder ergänzend zu diesem ausgewiesen. Anschaulich lässt sich der Median als der Wert „in der Mitte“ der Daten interpretieren. Bei geradem Stichprobenumfang ist der Median als die Mitte zwischen den beiden mittleren Werten definiert. Es seien x(1), x(2), . . . , x(n) die Beobachtungen aufsteigend nach ihrer Größe geordnet. x(1) ist also die kleinste Beobachtung und x(n) ist die größte Beobachtung. Dann ist der Median definiert als:
$$\tilde x=\begin{cases} x_\frac{n+1}{2} & n\text{ ungerade}\\ \frac {1}{2}\left(x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}\right) & n \text{ gerade.}\end{cases}$$
Beispiel: Es sei eine Stichprobe vom Umfang n = 8 mit folgenden Werten gegeben: 10,3,7,51,5,13,14,8
Zuerst werden die Werte entsprechend der Göße sortiert:
| x(1) | x(2) | x(3) | x(4) | x(5) | x(6) | x(7) | x(8) |
|---|---|---|---|---|---|---|---|
| 3 | 5 | 7 | 8 | 10 | 13 | 14 | 51 |
Der Stichprobenumfang ist gerade, so berechnet sich der Median als \(\tilde x= \frac{1}{2}(x_{4} + x_{5}) = 9\). Im Vergleich dazu ergibt sich für das Arithmetische Mittel ein Wert von \(\bar x = 12,33\).
Der Unterschied zwischen Median und dem arithemtischen Mittel wird im Beispiel vor allem durch die in Relation zu den restlichen Daten große Beobachtung „51“ verursacht, die den Mittelwert stark, den Median im Gegensatz dazu aber gar nicht beeinflusst.
Vor-/Nachteile des Medians:
+ unempfindlich gegenüber extremen Werten („robust“)
+ bei ordinalem oder metrischem Messniveau sinnvoll interpretierbar
- nutzt bei metrischem Messniveau nicht alle verfügbaren Informationen
Ausreißer und Extremwerte
Praktiker bezeichnen häufig Werte, die weit von der Masse der Daten entfernt liegen als Ausreißer. Dies ist streng genommen nicht immer korrekt. Es wird nach Extremwerten und Ausreißern unterschieden. Ausreißer sind Werte, die ungültig sind (z.B. durch Fehler bei der Übertragung der Daten oder durch bewusste Falschangaben zustande gekommen sind), während es sich bei Extremwerten um Werte handelt, die (weit) vom Zentrum der Daten entfernt liegen, die jedoch gültig sind (z.B. die Einkommen von Milliardären in der Einkommensstatistik).
Varianz und Standardabweichung
Arithmetisches Mittel und Median beschreiben die Lage der Daten. Ergänzend dazu sind Informationen über die Streuung der Daten von Interesse. Die Daten streuen wenig, wenn sich alle Beobachtungen auf einen relativ kleinen Bereich um den Mittelwert konzentrieren. Ist das Gegenteil der Fall, spricht man von starker Streuung. Da die Erfassung der Ausbreitung eines Datensatzes auf Abstandsmessungen basiert, können Streuungsparameter nur für metrisch skalierte Variablen berechnet werden. Als Standardmaß für die Streuung hat sich die sog. „Varianz“ etabliert. Die Varianz operationalisiert die Streuung als den mittleren quadrierten Abstand der Beobachtungen zum Zentrum der Daten (gemessen über das arithmetische Mittel):
$${s}^2=\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2=\overline{x^2}-\bar{x}^2$$
Der Wert der Varianz lässt sich über die Definition hinaus nicht unmittelbar intuitiv interpretieren. Dagegen ist die Varianz gut geeignet, um die Streuung zweier Merkmale miteinander zu vergleichen.
Gängige Statistikprogramm-Pakete verwenden in der Formel für die Varianz statt \(\frac{1}{n}\) meist den Term \(\frac{1}{n - 1}\) (sogennante korrigierte Stichprobenvarianz). Der Unterschied zwischen beiden Varianten ist bei großen Stichprobenumfängen vernachlässigbar.
Arbeitet man mit klassierten Daten, verwendet man eine Varianzformel bei der die einzelnen Beobachtungen xi durch die jeweiligen Klassenmitten mi ersetzt werden (ni entspricht der absoluten Häufigkeit, \(h_i = \frac{n_i}{n}\) der relativen Häufigkeit der jeweiligen Klasse):
$${s}^2=\frac{1}{n} \sum_{i=1}^k (m_i - \bar{x})^2\cdot n_i=\sum_{i=1}^k (m_i - \bar{x})^2\cdot h_i $$
Vor-/Nachteile der Varianz:
+ bekanntester Streuungsparameter
- wird stark durch extreme Werte in den Daten beeinflusst
- nur für Merkmale mit metrischem Messniveau geeignet (die Abstände zwischen den Werten müssen interpretierbar sein)
- hat eine andere Einheit als die Daten, weswegen die Varianz einer direkten Interpretation des Wertes nicht zugänglich ist
Der letzte Kritikpunkt lässt sich leicht durch eine Modifikation beheben: Wenn das Merkmal z.B. das in € gemessene Einkommen ist, hat die Varianz die kaum interpretierbare Einheit €2. Die Wurzel aus der Varianz (die sog. „Standardabweichung“) hat dann wieder dieselbe Einheit wie die Daten: \(s=\sqrt[2]{{s}^2}=\sqrt[2]{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2}\)
Quantile
Quantile dienen der genaueren Beschreibung von Lage und Streuung der Daten. Ein Quantil xp ist definiert als die kleinste Ausprägung x mit der Eigenschaft, dass mindestens p% der Beobachtungen höchstens so groß sind wie x. Quantile lassen sich teilweise sehr einfach aus der Häufigkeitstabelle ablesen. Als Beispiel wird auf die Häufigkeitstabelle aus diesem Kapitel verwiesen.
Ein Quantil xp lässt sich ablesen, in dem man die Spalte der kumulierten relativen Häufigkeiten von oben nach unten durchgeht. Das Quantil entspricht der Merkmalsausprägung in der Zeile, in der die kumulierte relative Häufigkeit erstmalig größer oder gleich p ist. Als Beispiel sollen das 5%-, 25%- und das 75%-Quantil bestimmt werden:
a) x0,05 = 1: 5% der befragten Kunden sind sehr unzufrieden mit dem Produkt
b) x0,25 = 3: 25% der Kunden bewerten das Produkt bestenfalls neutral
c) x0,75 = 4: 75% der Kunden waren mit ihrem Besuch bestenfalls eher zufrieden
In den Fällen a) und c) aus dem Beispiel stimmt der Wert der kumulierten relativen Häufigkeit exakt mit p überein. Im Fall b) wird mit x = 3 die kleinste Ausprägung verwendet, für die die kumulierte relative Häufigkeit größer als p ist. Viele Statistikprogramme „interpolieren“ in dieser Situation und geben einen Wert aus, der – abhängig vom verwendeten Verfahren – zwischen 2 und 3 liegt. Im Beispiel wurde ein kleiner Datensatz verwendet. Quantile sind speziell bei größeren Datensätzen geeignet, um einen Eindruck über die Verteilung der Daten zu vermitteln. So werden z.B. beim Einkommen häufig 1%-, 5%-, 10%-, 25%-, 50%-, 75%-, 90%-, 95%-, 99%- und 99.9%-Quantil angegeben. Die „unteren“ Quantile werden zur Definition einer relativen Armutsschranke genutzt. Im Bezug auf Einkommensdaten werden oft die Lorenzkurve und der Gini-Koeffizient verwendet, um sich ein Bild der Verteilung des Merkmals zu verschaffen. Folgende spezielle Quantile werden in der Praxis häufig verwendet:
• Dezile: x0,1, x0,2, . . . , x0,9
• Quartile: x0,25, x0,5, x0,75 (Viertelung des Datensatzes)
• Median: x0,5 (Halbierung des Datensatzes)
Der Begriff „Median“ ist in der Praxis sowohl für das 50%-Quantil als auch für den Median im Sinne der Definition aus vorherigem Abschnitt Median gebräuchlich. In kleinen Stichproben können sich die Werte des Quantils und des Lageparameters jedoch durchaus unterscheiden. Mit wachsendem Stichprobenumfang wird ein ggf. existierender Unterschied jedoch immer kleiner und verschwindet asymptotisch komplett (wenn der Stichprobenumfang gegen unendlich geht).
Interquartilsabstand
Ein weiteres Streuungsmaß ist der Interquartilsabstand. Der Interquartilsabstand (kurz: „IQR“ für „interquartile range“) ist der Abstand zwischen dem 25%-Quantil (auch „unteres Quartil“ genannt) und dem 75%-Quantil (auch „oberes Quartil“ genannt): IQR = x0,75 − x0,25
Vor-/Nachteile des Interquartilsabstands:
+ anschaulich interpretierbar als die Breite des Bereichs in dem die mittleren 50% der Beobachtungen liegen
+ relativ unempfindlich gegenüber extremen Werten („robust“)
- bei ordinalem oder metrischem Messniveau sinnvoll interpretierbar
- nutzt bei metrischem Messniveau nicht alle verfügbaren Informationen
Der Interquartilsabstand spielt eine wichtige Rolle in der grafischen Auswertung von Daten insbesondere bei den sogenannten Boxplots.
Zusammenhangsmaße
Kovarianz
Neben Lage- und Streuungsparametern einzelner Merkmale sind Maße für den Zusammenhang mehrerer Variablen von Interesse. Um zu überprüfen ob zwischen zwei Variablen x und y ein Zusammenhang besteht, kann als erstes Maß die Kovarianz verwendet werden. Die Kovarianz stellt eine Verallgemeinerung der Varianz dar, da die Varianz eines Merkmals auch als Kovarianz des Merkmals mit sich selbst ausgedrückt werden kann. Auf Grund dieses Zusammenhangs teilt die Kovarianz auch die Eigenschaft der Varianz, dass der berechnete Wert nicht direkt in der Höhe interpretiert werden kann. Ein negativer Wert entspricht einem negativen Zusammenhang (kleine Werte von x gehen mit großen Werten von y einher und andersherum), ein positiver Wert deutet darauf hin, dass große Werte von x mit großen Werten von y einhergehen.
$$s_{xy}=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})=\overline{xy} - \bar x \cdot \bar y, \text{wobei } \overline{xy}=\frac{1}{n}\sum_{i=1}^nx_iy_i $$
Es ist wichtig, zu beachten, dass die Kovarianz skalenabhängig ist.
Korrelationskoeffizient nach Bravais-Pearson
Der Korrelationskoeffizient nach Bravais-Pearson wird verwendet, um die Stärke eines linearen Zusammenhangs zweier metrisch skalierter Variablen zu quantifizieren. Nur die Kovarianz der Merkmale zu betrachten reicht nicht aus, da diese skalenabhängig ist und somit durch Lineartransformationen beliebig vergrößert oder verkleinert werden kann. Um diese Eigenschaft zu beseitigen, wird die Kovarianz auf die jeweiligen Standardabweichungen der Variablen bezogen.
$$\operatorname{Kor}_e(x,y) := \varrho_e(x,y) := r_{xy} := \frac{ \sum_{i=1}^n(x_i-\bar x)(y_i-\bar y) }{ \sqrt{ \sum_{i=1}^n(x_i-\bar x)^2\cdot \sum_{i=1}^n(y_i-\bar y)^2 }}$$
Die Maßzahl (geschrieben rx,y ) misst den linearen Zusammenhang zwischen zwei Merkmalen x und y und kann Werte zwischen -1 und +1 annehmen. Bei rx,y = 1 lässt sich die Beziehung zwischen x und y in der Form y = a + bx mit b > 0 angeben. Bei rx,y = −1 gilt analog y = a + bx mit b < 0. Bei r = 0 existiert keine Beziehung der Form y = a + bx zwischen x und y. Dies bedeutet allerdings nur, dass kein linearer Zusammenhang besteht. Ein intuitives Beispiel für einen Korrelationskoeffizienten von Null bei perfekter nichtlinearer Korrelation stellt die Funktion y = f(x) = x2 dar. Jeder Wert von y ist durch die Funktion bei gegebenem x-Wert eindeutig bestimmt. Trotzdem spiegelt sich das im Maß des linearen Zusammenhangs nicht wider.
Zur Veranschaulichung des Konzepts wird der ALLBUS-Datensatz herangezogen. Im grafischen Analyseteil dieses Artikels werden Streudiagramme (oder engl. Scatterplot) vorgestellt, welche ebenso wie Korrelationskoeffizienten einen Eindruck des Zusammenhangs zweier Merkmale liefern. Je stärker sich die Punktewolke um eine aufsteigende (absteigende) Gerade gruppiert, desto näher liegt der Wert des Koeffizienten bei +1 (-1). Für die ersten 300 Befragten des Beispieldatensatzes ergibt sich ein Wert des Zusammenhangs von 0,653. Wie erwartet gehen mit kleinen (großen) Werten des Merkmals Größe tendenziell kleine (große) Werte des Merkmals Gewicht einher.
Rangkorrelationskoeffizient nach Spearman
Sofern die Variablen x und y zumindest ordinales Messniveau haben, lässt sich der Korrelationskoeffizient nach Spearman (auch „Rangkorrelationskoeffizient“ genannt) berechnen.
Im Vergleich zum Korrelationskoeffizienten von Pearson ist der Rangkorrelationskoeffizient wesentlich weniger von einzelnen Ausreißern beeinflusst. Gemessen wird der monotone Zusammenhang zweier Variablen. Der Koeffizient nimmt tendenziell hohe Werte an, wenn mit hohen Werten der einen auch hohe Werte der anderen Variable einhergehen.
Die Berechnung dieses Maßes beruht im Gegensatz Pearsons Maß nicht auf den Werten der Beobachtungen selbst, sondern auf ihren Rängen. Bei dieser Methode erhält jede Ausprägung einen Rang gemäß ihrer Größe zugewiesen, d.h. der kleinste Wert erhält jeweils den Rang eins, der zweitkleinste den Rang zwei usw.
Treten gleiche Werte auf (sogenannte Bindungen), werden mittlere Ränge vergeben. Beispielsweise erhält man für die beobachteten Werte von x folgende Ränge:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ausprägung | 7 | 3,2 | 8 | 24,6 | 12,5 | 7 | 10 | 2 | 10 | 26,3 |
| Rang | 3,5 | 2 | 5 | 9 | 8 | 3,5 | 6,5 | 1 | 6,5 | 10 |
Nach der Rangbestimmung für beide Merkmale kann anhand folgender Formel der Korrelationskoeffizient bestimmt werden:
$$r_s = \frac{\sum_{i}(rg(x_i)-\overline{rg}_x)(rg(y_i)-\overline{rg}_y)} {\sqrt{\sum_{i}(rg(x_i)-\overline{rg}_x) ^2}\sqrt{\sum_{i}(rg(y_i)-\overline{rg}_y)^2}} = \frac { \frac{1}{n} \sum_{i}(rg(x_{i}) rg(y_{i})) - \overline{rg_x rg_y} }{s_{rg_x} s_{rg_y}}$$
$$= \frac {\operatorname{Cov}(rg_{x},rg_{y} )} { s_{rg_x} s_{rg_y} }.$$
Sollten alle x-Werte und y-Werte in sich unterschiedlich sein, d.h. keine Bindungen auftreten, vereinfacht sich die Berechnung folgendermaßen:
$$r_s = 1 - \frac{6 \sum_{i} d_i^2} { n \cdot (n^2 – 1)},$$
wobei \(d_i\) die jeweilige Differenz zwischen den Rängen von x und y einer Beobachtung angibt.
Grafische Auswertung
In der deskriptiven Statistik ist neben der Beschreibung des Datensatzes mit Hilfe von Häufigkeitstabellen, sowie Lage-/Streuungsparametern, die Visualisierung der Daten bedeutsam. Für die Darstellung der Daten gibt es viele unterschiedliche Möglichkeiten. Im folgenden Abschnitt werden einige Visualisierungsmöglichkeiten vorgestellt und auf den ALLBUS-Datensatz angewendet.
Balken/- Kreisdiagramm
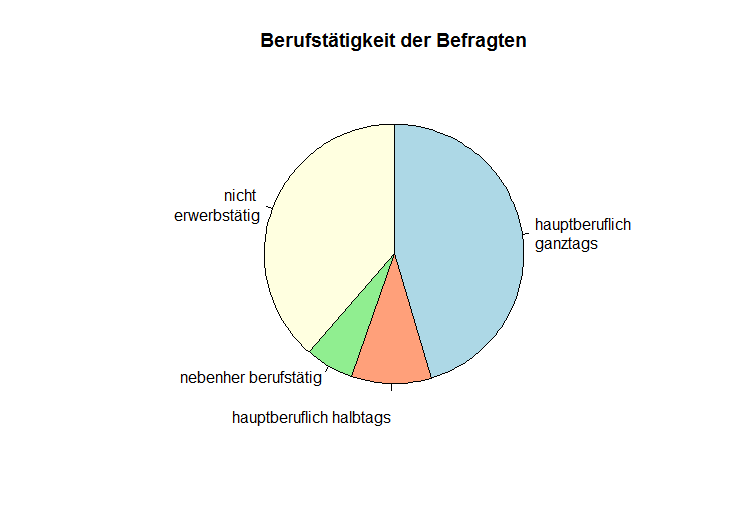
Besonders einfach zu lesen – und aus den Medien hinreichend bekannt – sind Balken und Kreis- bzw. Tortendiagramme. Diese Diagramme lassen sich einfach aus einer Häufigkeitstabelle generieren. Wahlweise können beim Balkendiagramm die absoluten oder die relativen Häufigkeiten abgetragen werden. Beim Tortendiagramm werden allerdings immer die relativen Häufigkeiten dargestellt, da „ein Ganzes“ in seine Anteile unterteilt wird. Die Größe des Winkels lässt sich dabei aus der Multiplikation von 360° mit dem entsprechendem Anteil bestimmen.

Berufstätigkeit der Befragten
In diesem Balkendiagramm werden die absoluten Häufigkeiten für die unterschiedlichen Arten von Berufstätigkeit (hauptberuflich ganztags, hauptberuflich halbtags, nebenher berufstätig, nicht erwerbstätig) dargestellt.
Berufstätigkeit der Befragten
In diesem Kreisdiagramm wird, wie in dem vorherigen Balkendiagramm, die Berufstätigkeit der Befragten dargestellt. Dabei werden die relative Häufigkeit für die unterschiedlichen Arten der Berufstätigkeit visualisiert. Entsprechend den relativen Häufigkeiten (relative Häufigkeit bestimmt die Größe des Winkels) wird ein "Ganzes" in mehrere Stücke zerteilt.
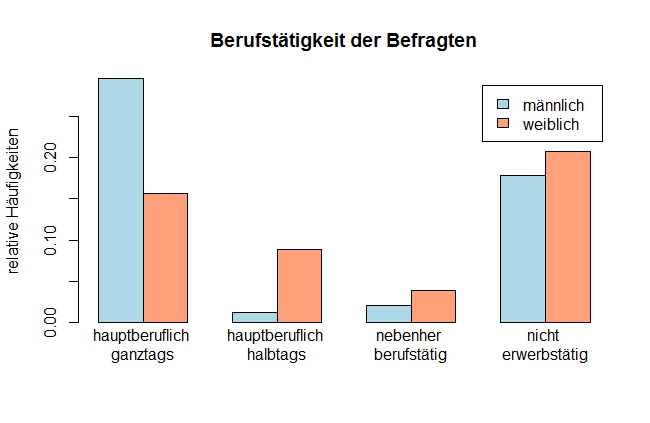
Gruppierte Balkendiagramme eignen sich besonders, wenn es inhaltlich sinnvoll ist, innerhalb eines Merkmals zwischen verschiedenen Subgruppen zu unterscheiden. So wird in dem hier erstellten gruppierten Balkendiagramm die relativen Häufigkeiten im Bezug auf Berufstätigkeit nach Geschlechtern getrennt dargestellt. Vergleichend mit dem vorherigem Balkendiagramm können hier zusätzlich Schlüsse über das unterschiedliche Verhalten von Männern und Frauen im Bezug auf die Berufstätigkeit gezogen werden.
Berufstätigkeit der Befragten
Dieses gruppierte Balkendiagramm stellt die relativen Häufigkeiten für die unterschiedlichen Arten von Berufstätigkeit getrennt nach Geschlecht dar. Es eignet sich so gut, um Unterschiede zwischen beiden Geschlechtern deutlich zu machen.
Anwendungshinweise
- geeignet für Merkmale mit nominalem oder ordinalem Messniveau, die nur wenige Ausprägungen haben
- bei metrischem Messniveau sollten Stabdiagramme verwendet werden
- insbesondere Kreisdiagramme werden schnell unübersichtlich, wenn es zu viele Segmente gibt (eine Lösung ist das Verwenden anderer Möglichkeiten der grafischen Darstellung oder das Zusammenfassen unterschiedlicher Merkmale)
Stabdiagramm
Das Stabdiagramm enthält ebenfalls Balken bzw. Linien für jede Ausprägung, deren Höhe von der absoluten oder relativen Häufigkeit des Auftretens der jeweiligen Ausprägung abhängt. Anders als beim Balkendiagramm spiegelt die Entfernung der Balken zueinander beim Stabdiagramm jedoch die Abstände der Ausprägungen wider. Dies setzt natürlich voraus, dass diese überhaupt interpretierbar sind, was nur bei metrischem Messniveau gegeben ist. In dem hier durchgeführten Beispiel zu der Anzahl der Arztbesuche unterschiedlicher befragter Personen (ALLBUS-Datensatz) zeigt sich der Unterschied zu einem Balkendiagramm deutlich. Beim Balkendiagramm wäre keine Lücke zwischen beispielsweise 21 und 24 Arztbesuchen, sondern es wären die Häufigkeiten für beide Anzahlen von Arztbesuchen direkt nebeneinander aufgetragen.
Der Vorteil des Stabdiagramms liegt darin, dass nun die Abstände der einzelnen metrischen Merkmalsausprägungen (Anzahl der Arztbesuche) auf einer Skala dargestellt werden, sodass für den Betrachter die Abstände zwischen den diskreten Merkmalen verdeutlicht werden.

Anzahl der Artzbesuche der Befragten
In diesem Ausschnitt des Stabdiagramms für die Anzahl der Arztbesuche sind die absoluten Häufigkeiten über die Anzahl der Arztbesuche aufgetragen. Auf der Abszissenachse sind dabei die Anzahl der Arztbesuche aufgetragen. Diese sind auf einer Skalar dargestellt, sodass die Abstände zwischen diesem diskreten Merkmal deutlich werden.
Anwendungshinweise
- geeignet für diskrete Merkmale mit metrischem Messniveau
- wenn das Stabdiagramm durch zu viele Balken unübersichtlich wird oder sehr viele Fälle mit der absoluten Häufigkeit von 1 auftreten, ist das Histogramm eine Alternative
Histogramm
Während das Stabdiagramm die Informationen aus der Häufigkeitstabelle eines unklassierten metrischen Merkmals visualisiert, erfüllt das Histogramm den selben Zweck für klassierte metrische Merkmale. Für jede Klasse wird ein Balken gezeichnet, dessen Breite und Position durch die Klassenunter- und Obergrenze bestimmt werden. Die Höhe des Balkens entspricht der absoluten Häufigkeit in der Klasse, der relativen Häufigkeit in der Klasse oder der Häufigkeitsdichte. Letztere ist eine einfache Transformation der relativen Häufigkeiten, bei der diese für jeden Balken ins Verhältnis zur jeweiligen Klassenbreite gesetzt werden. Wird auf der Ordinate im Histogramm die Häufigkeitsdichte abgetragen, entspricht die Fläche unter jedem Balken der relativen Häufigkeit der korrespondierenden Klasse, die Gesamtfläche aller Balken ist immer eins.
In dem hier gezeigten Beispiel wurden die Personen aus dem verwendeten Datensatz in 13 Klassen nach ihrem Gewicht eingeteilt.

Gewicht der Befragten
In diesem Histogramm ist die Häufigkeitsdichte über das Gewicht aufgetragen. Dazu wird das metrische Merkmal (Gewicht) in Klassen eingeteilt (hier in 13 gleich große Klassen), die Höhe eines solchen Balkens entspricht hier der Häufigkeitsdichte.
Die Verwendung von unterschiedlichen Klassenbreiten erweist sich als sinnvoll, um Bereiche mit hohen Häufigkeitsdichten besser zu differenzieren. So wurde beispielsweise in den Bereichen zwischen 60 und 90 Kilogramm eine Klassenbreite von 5 Kilogramm gewählt um eine bessere Differenzierung in diesem Bereich zu ermöglichen.

Gewicht der Befragten
Wie in dem vorherigen Diagramm wird auch hier die Häufigkeitsdichte über das Gewicht aufgetragen. Der Unterschied zwischen beiden Diagrammen liegt darin, dass die Klassenbreiten in diesem Histogramm variieren, sodass in den Bereichen mit kleinen Klassenbreiten eine bessere Differenzierung möglich ist.
Anwendungshinweise
- geeignet für stetige Merkmale mit metrischem Messniveau
- insbesondere bei Klassen mit unterschiedlicher Breite sollte auf der Ordinate die Häufigkeitsdichte abgetragen werden
- die Wahl der Klassenanzahl/Klassenbreite kann wesentlichen Einfluss auf das Aussehen der Grafik haben und unterliegt einer gewissen Willkür
Boxplot
Boxplots visualisieren die Quantile des Merkmals. Es wird eine Box gezeichnet, die durch das untere und das obere Quartil begrenzt wird (siehe Interquartilsabstand). In der Box wird die Position des 50%-Quantils durch eine Linie markiert. Von den Enden der Box wird eine Linie zum Minimum und auf der anderen Seite zum Maximum gezogen. Diese Linien werden als „Whiskers“ („Schnurrhaare“) bezeichnet. Ein Boxplot visualisiert somit in kompakter Form die Position von Minimum, 25%-Quantil, 50%-Quantil (bzw. Median), 75%-Quantil und Maximum. Aufgrund der platzsparenden Form der Darstellung lassen sich mit Hilfe von Boxplots problemlos mehrere Merkmale vergleichen.
Das hier verwendete Beispiel vergleicht die Verteilung der Größe von männlichen und weiblichen Befragten des ALLBUS-Datensatzes.

Größenvergleich zwischen männlichen und weiblichen Befragten
Hier sind zwei Boxplots dargestellt, welche beide die Quantile des Gewichts visualisieren. Der eine Boxplot stellt die Quantile für die weiblichen Befragten der andere für die männlichen Befragten dar, sodass anhand dieser beiden Boxplots Vergleiche zwischen beiden Gruppen angestellt werden können.
Anwendungshinweise
- geeignet für Merkmale mit ordinalem oder metrischem Messniveau
- sehr gut geeignet, um mehrere Merkmale miteinander zu vergleichen oder die Ausprägungen eines Merkmals separiert nach einer Gruppierungsvariable zu betrachten
- aus dem Boxplot können unmittelbar der Median (bzw. das 50%-Quantil) und der IQR (entspricht der Länge der Box) abgelesen werden
Vorsicht
Einige Statistikprogramme prüfen nach einer bestimmten (aber nicht einheitlichen) Regel, ob Beobachtungen am Rand der Verteilung als Extremwerte einzustufen sind. Fällt die Prüfung positiv aus, werden diese Beobachtungen als einzelne Punkte gekennzeichnet und die Whiskers lediglich bis zu den äußeren Beobachtungen gezogen, die nicht als Extremwerte eingestuft wurden.
Beispielsweise in der Statistik-Software R wird unter Standardeinstellung die Länge des Whiskers beschränkt durch den Wert des 1,5 fachen IQRs (Ausreißerregel von Tukey). Kleinere und größere Werte werden dann als Ausreißer angesehen und als Punkte außerhalb der Whiskers gekennzeichnet, wie in der folgenden Abbildung zu sehen.
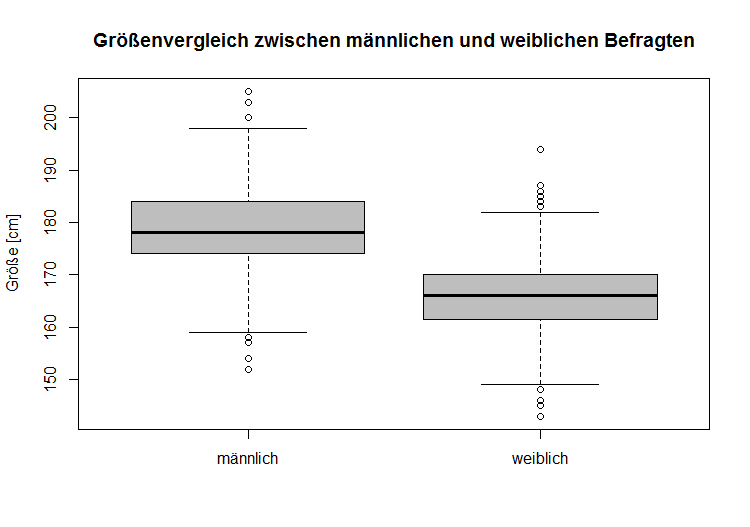
Größenvergelich zwischen männlichen und weiblichen Befragten
Wie in den vorherigen Boxplots sind auch hier die Quantile für die Größe dargestellt. Allerdings werden hier die Whiskers nicht immer bis zum Minimum und Maximum durchgezeichnet. Fällt nämlich eine Prüfung auf Extremwerte (z.B.: Ausreißerregel von Tukey, die für R verwendet wird) positiv aus, so wird der Whisker nur bis zur äußersten Beobachtung, die kein Extremwert ist, gezogen.
Streudiagramm
Kontingenztabellen sind geeignet, um den Zusammenhang zwischen zwei diskreten Merkmalen zu untersuchen. Für die Untersuchung von Zusammenhängen zwischen stetigen Merkmalen eignen sich Kontingenztabellen jedoch nicht. Das Streudiagramm ist in diesem Fall die richtige Wahl.
Aus dem vorliegenden Datensatz werden Punkte in ein Koordinatensystem gezeichnet, wobei auf der Abszisse die Größe in Zentimeter und auf der Ordinate das Gewicht in Kilogramm aufgetragen ist. Das so entstandene Streudiagramm gibt den zu erwartenden Zusammenhang zwischen Größe und Gewicht wider. In dem hier gewählten Beispiel wurde dieser Zusammenhang, um die Übersichtlichkeit zu wahren, nur für die ersten 300 Befragten des Datensatzes durchgeführt.

Größe und Gewicht von 300 Befragten
Sofern man davon ausgeht, dass zwischen den im Streudiagramm dargestellten Merkmalen auch ein kausaler Zusammenhang besteht, ist es üblich, das Merkmal, von dem der Einfluss ausgeht (das sog. „unabhängige Merkmal“), auf der Abszisse und das Merkmal, welches beeinflusst wird („abhängiges Merkmal“), auf der Ordinate abzutragen.
Bildergalerie

|

|

|

|

|

|

|

|

|

|

|

|

|

|
||
- Keine Stichwörter