- Erstellt von Ann-Kristin Kreutzmann, zuletzt aktualisiert von Benedict Günter am 25.07.2024 Lesedauer: 20 Minute(n)
Die ordinale Regression umfasst Modelle, deren Zielvariable ordinal skaliert ist, d.h. es liegt eine kategoriale Variable vor deren Ausprägungen eine Rangordnung vorweisen, z.B. Schulnoten („1“, „2“, „3“, …,“6“), Ausprägung einer Krankheit („gesund“, „leicht krank“, „mittel krank“, „schwer krank“) oder Zufriedenheit mit einem Produkt (Skala von 0 bis 10). Dabei gilt, dass die Abstände zwischen den Ausprägungen nicht interpretierbar sind, d.h. dass z.B. der Abstand zwischen den Schulnoten „1“ und „2“ nicht dem Abstand der Noten „4“ und „5“ entsprechen muss, weshalb die Nutzung von linearen Regressionsmodellen unangemessen ist. Anstelle von ordinalen Regressionsmodellen könnten Daten mit ordinaler Skalierung auch mit multinominalen Logitmodellen (Logistische Regression (Logit-Modell)) untersucht werden. Jedoch würde in diesem Fall die Information über die Reihenfolge der kategorialen Ausprägungen nicht genutzt werden, was zu ineffizienten Schätzern führen würde. Je nachdem welche Annahme über die Verteilung der Fehlerterme getroffen wird, sprechen wir von geordneten logistischen Regressionen (logistisch verteilt) oder geordneten Probitregressionen (standardnormalverteilt). Wenn eine höhere Kategorie nur erreicht werden kann, wenn eine niedrigere schon erreicht wurde, können sogenannte sequentielle Modelle genutzt werden. Ein Beispiel ist die Variable Dauer der Arbeitslosigkeit unterteilt in verschiedene Kategorien: "1 Jahr", "2 Jahre", "mehr als 2 Jahre". Eine Person kann nur zwei Jahre arbeitslos sein, wenn sie schon ein Jahr arbeitslos war.
Dieser Artikel ist analog zum Artikel Logistische Regression (Logit-Modell) aufgebaut.
Inhaltsverzeichnis
Variablen und deren Zusammenhang
| abhängige Variable (\(y\)) | ordinal (Reihenfolge in Ausprägungen liegt vor) |
| unabhängige/n Variable/n (\(x\)) | beliebiges Skalenniveau (die Skalenniveaus der einzelnen \(x_1,...,x_P\) dürfen sich auch unterscheiden, liegt eine kategorische Variable vor, so muss eine Zerlegung in Dummy-Variablen stattfinden) |
Das Ziel der ordinalen Regression ist die Vorhersage von Wahrscheinlichkeiten für das Auftreten der einzelnen Kategorien in Abhängigkeit von Kovariablen.
Ein Beispiel für die Anwendung der ordinalen Regression stellen Likert-Skalen dar. Sie sind ein Spezialfall von Ordinalskalen, das heißt die Werte einer solchen Skala sind verschiedenartig und lassen sich einer eindeutigen Rangfolge zuordnen. Likert-Skalen werden genutzt, um persönliche Einstellungen (Zustimmung/Ablehnung) von Individuen zu messen, weshalb sie häufig als Antwortskalen in Umfragen verwendet werden. Typischerweise haben sie 3, 5, 7 oder 11 Werte.
Typische Likert-Skalen sind:
- überhaupt nicht (1) - wenig (2) - mittel (3) - stark (4) - sehr stark (5)
- trifft zu (1) - teils/teils (2) - trifft nicht zu (3)
Die erste Variable hat 5 Kategorien, die mit den Werten 1, 2, 3, 4 und 5 kodiert werden.
Es mag die Frage aufkommen, ob Likert-Skalen nicht auch mit linearen Regressionsmodellen analysiert werden können. Likert-Skalen stellen keine metrische abhängige Variable dar, daher sollte von der Nutzung von linearen Regressionsmodellen in der Regel abgesehen werden, es gibt jedoch einige Ausnahmen wie z.B. eine relativ große Anzahl an Kategorien (z.B. 11). Für weitere Informationen siehe hier.

Motivation über Schwellenwertmodelle
Ordinale Regressionsmodelle werden über Schwellenwertmodelle motiviert. Eine nicht beobachtbare Hintergrundvariable (auch latente Variable genannt) \(y^*\) wird angenommen, die metrisch ist. Das Modell lautet: \(y^*_i=x'_i\beta+\epsilon_i, \quad i=1,\dots,n\). Hierbei wird für die Verteilung der \(\epsilon_i\) eine Verteilungsfunktion \(F\) mit Erwartungswert 0 angenommen, die symmetrisch um die 0 verteilt ist. Häufig wird für \(F\) die Standardnormalverteilung angenommen. In diesem Spezialfall erhält man das Probit-Modell.
Anstatt den Zusammenhang zwischen der beobachtbaren ordinalen Variable und den Einflussvariablen zu schätzen, wird der Zusammenhang zwischen der latenten metrischen Variable und den Einflussvariablen geschätzt. Dabei stellen die beobachtbaren Kategorien (mit endlicher Anzahl an Kategorien (m + 1)) das Überschreiten der Schwelle der latenten metrischen Variablen dar:
$$y_i={\begin{cases}0\ ,&{\text{für}}&-\infty<y^*_i\leq\alpha_1\ ,\\1\ ,&{\text {für}}&\alpha_1<y^*_i\leq\alpha_2\ ,\\&\vdots\\m\ ,&{\text{für}}&\alpha_m<y^*_i\leq\infty\end{cases}}$$
\(\alpha_j \) (\( j = 1, 2, ..., m \)) stehen für geordnete Schwellenwerte, die neben den \( \beta \) auch geschätzt werden müssen. Weil der Wertebereich der latenten Variable nicht bekannt ist, nimmt man \( \alpha_0 = - \infty \) und \( \alpha_{m+1} = \infty \) an.
Die folgende Abbildung zeigt den Zusammenhang für eine Likert-Skala mit 3 Kategorien und einer Einflussvariablen \(x \). Der rote Punkt hat im ersten Bild die Koordinaten \( x = 5,9 \) und \(y^* = 0.05 \). Da \( y^*\) zwischen \(\alpha_1 = -4\) und \( \alpha_2 = 1 \) liegt, nimmt der \(y\) - Wert im zweiten Bild einen Wert von \( 2 \) an.
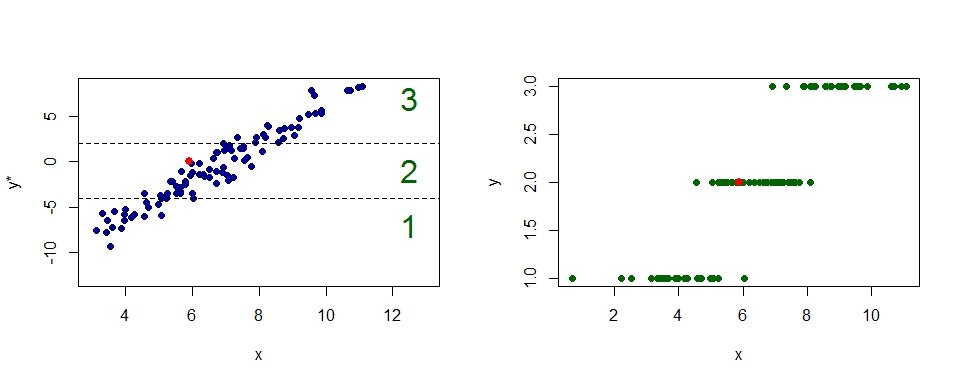
Bei der ordinalen Regression werden die Wahrscheinlichkeiten für das Auftreten von Kategorien \( j = 1, 2, ..., m \) durch erklärende Variablen \(x_1, x_2, ..., x_P\) mit Hilfe von bedingten kumulierten Wahrscheinlichkeiten \(P(y \leq j |x_i) = P(Y_i = 1 |x_i) + ... + P(Y_i = j |x_i)\) geschätzt, daher spricht man auch von kumulativen (Logit-/Probit-) Modellen.
Weil die Wahrscheinlichkeit für das Eintreten der höchsten Kategorie oder einer niedrigeren 100% beträgt ( \( P(Y_i \leq m |x_i) = 1 \) ), werden nur \(m - 1\) Kategorien modelliert, damit eine Überparametrisierung verhindert werden kann. Als Referenzkategorie wird im ordinalen Logitmodell entweder die kleinste oder größte Kategorie der Zielvariable ausgewählt.
Aus der Modellannahme über die latente Variable und das Schwellenwertkonzept ergibt sich das kumulative Modell mit Verteilungsfunktion \( F \)
\( P (Y_i = 1 | x_i) = F(\alpha_1 - x'_i \beta) \)
\(P (Y_i = j | x_i) = F(\alpha_j - x'_i \beta) - F(\alpha_{j - 1} - x'_i \beta),\) \( j = 2, ..., m - 1 \)
\(P (Y_i = m | x_i) = 1 - F(\alpha_{m - 1} - x'_i \beta) \)
Die Wahl von \( F\) bestimmt, ob ein Logit, Probit oder anderes Modell vorliegt.
Abbildung
Das kumulative Logit-Modell
Die Wahl der logistischen Funktion \( F(x) = \frac{e^x}{1+ e^x} \) resultiert im kumulativen Logit-Modell - auch Proportional Odds Modell genannt -
\[ P(Y_i \leq j | x_i) = \frac{exp(\alpha_j - x'_i \beta)}{1 + exp(\alpha_j - x'_i \beta)}\]
oder
\[ log \left( \frac{P(Y_i \leq j | x_i)}{P(Y_i > j | x_i)} \right) = log \left( \frac{P(Y_i \leq j | x_i)}{1 - P(Y_i \leq j | x_i)} \right) = \alpha_j - x'_i \beta \]
Während die Schwellenparameter \( \alpha_j \) kategorienspezifisch sind und monoton in \(j \) steigen, gehen die Einflussvariablen \( x_i \) global ins Modell ein und führen zu globalen Regressionskoeffizienten \( \beta \). Die Parameter \( \alpha_j \) und \( \beta \) werden durch die Maximum-Likelihood (ML) Methode geschätzt. Aus Identifikationsgründen darf die Designmatrix (Matrix der erklärenden Variablen) keinen Intercept enthalten, sonst könnten die Schwellenwerte davon nicht unterschieden werden und blieben unidentifiziert. Die ML-Schätzer sind konsistent, asymptotisch effizient und asymptotisch normalverteilt.
Geordnete Probitregression
Die geordnete Probitregression folgt den gleichen Überlegungen wie die geordnete logistische Regression. Der Unterschied liegt in der Annahme über die Verteilung der Fehlerterme, welche bei der Probitregression als standard normal verteilt angenommen wird. Weitere Linkfunktionen sind z.B. log-log, kumulative inverse Cauchy-Verteilung, etc.
Sequentielle Modelle
Neben kumulativen Modellen stellen sequentielle Modelle eine wichtige Modellklasse der ordinalen Regression dar. Sequentielle Modelle werden genutzt, wenn eine höhere Kategorie nur erreicht werden kann, wenn eine niedrigere schon erreicht wurde, d.h. wenn die Kategorien nur sukzessiv/schrittweise erreicht werden können. Ein Beispiel ist die abhängige Variable Dauer der Arbeitslosigkeit unterteilt in verschiedene Kategorien: "1 Jahr", "2 Jahre", "mehr als 2 Jahre". Eine Person kann nur mehr als zwei Jahre arbeitslos sein, wenn sie schon zwei Jahre arbeitslos war.
Der schrittweise Übergang zwischen den Kategorien wird dabei durch dichotome Zusammenhänge mit Hilfe von binären Regressionsmodellen modelliert. Der Prozess, der nur zur Modellierung dient, startet mit \(Y_i=1\) und modelliert den Übergang zu \(Y_i=1\) durch ein binäres Modell:
\[ P(Y_i=1 |x_i) = F(\alpha_1 + x'_i\beta)\]
Wenn die Zielvariable \(Y\) in der ersten Kategorie verbleibt, endet der Prozess, ansonsten geht es sukzessive weiter mit dem nächsten Übergang von \(Y_i =2\) zu \(Y_i >2\):
\[ P(Y_i=2 |Y_i \geq 2, x_i) = F(\alpha_2 + x'_i\beta)\]
Der entsprechend \(j\)-te Übergang sieht wie folgt aus:
\[ P(Y_i=j |Y_i \geq j, x_i) = F(\alpha_j + x'_i\beta), \qquad \forall j=1,...,m\]
Wenn ein Übergang nicht stattfindet, endet der schrittweise Mechanismus, d.h. eine Kategorie \(j \) ( \( j = 1, 2, ..., m\) ) ist erreicht.
Wie bei den kumulativen Modellen bestimmt die Wahl der Verteilungsfunktion \(F\) das tatsächliche Modell. Bei der logistischen Verteilungsfunktion, spricht man vom sequentiellen Logit-Modell, während ein sequentielles Probit-Modell vorliegt, wenn die Standardnormalverteilung als Verteilungsfunktion \(F\) gewählt wird. Das Modell kann erweitert werden, indem Koeffizienten \(\beta\) genutzt werden, die kategorienspezifische Effekte beschreiben.
Im folgenden Artikel werden sequentielle, sowie Probitmodelle, nicht im Detail ausgeführt. Der Fokus liegt auf kumulativen Logit-Modellen, die in der praktischen Anwendung am häufigsten genutzt werden. Einen Überblick über die Unterschiede von kumulativen Logit-Modellen und sequentiellen Modellen gibt der verlinkte Artikel.
Einführung in das Beispiel
Einführung in das Beispiel: Schulabschluss Die abhängige Variable Schulabschluss ("SCHULABSCHLUSS") ist ordinal skaliert und hat die Ausprägungen "HAUPT" für Volks-/ Hauptschulabschluss bzw. Polytechnische Oberschule mit Abschluss 8. oder 9. Klasse, "MITTEL" für Mittlere Reife, Realschulabschluss bzw. Polytechnische Oberschule mit Abschluss 10. Klasse und "ABI" für Fachhochschulreife (Abschluss an einer Fachoberschule etc.)/Abitur bzw. Erweiterte Oberschule mit Abschluss 12. Klasse (Hochschulreife). In diesem Beispiel sind die erklärenden Variablen eine Dummy-Variable für das Geschlecht ("GESCHL", 1 = männlich, 2 = weiblich), eine metrisch skalierte Variable "NETTO", die das Nettoeinkommen einer Person misst und eine Faktorvariable Schulabschluss des Vaters "SCHULABSCHLUSS_V" mit den gleichen Ausprägungen wie die der abhängigen Variablen. Die Variablen stammen aus einem vereinfachten Datensatz der ALLBUS-Umfrage (siehe Beispieldatensätze und Beispielprogramme). |
|---|
Um einen ersten Überblick über die verwendeten Variablen zu gewinnen, werfen wir einen Blick auf einfache deskriptive Statistiken der genannten Variablen. Die folgenden Tabellen beschreiben die Häufigkeiten der Faktorvariablen und einige Eckdaten über die metrische Variable "NETTO".
SCHULABSCHLUSS
| HAUPT | MITTEL | ABI |
|---|---|---|
| 603 | 780 | 897 |
GESCHL
| MAENNLICH | WEIBLICH |
|---|---|
| 1188 | 1092 |
SCHULABSCHLUSS_V
| HAUPT | MITTEL | ABI |
|---|---|---|
| 1428 | 415 | 437 |
NETTO
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 37 | 800 | 1300 | 1597 | 2000 | 60000 |
Interpretation der Parameter und anderer Kenngrößen
Die Interpretation der marginalen Wahrscheinlichkeitseffekte gestaltet sich etwas schwieriger als in einem Multinomialen Modell. Der Effekt hängt sowohl vom geschätzten Parameter, als auch von der Differenz von Wahrscheinlichkeitsdichten ab.
Es lassen sich jedoch auch wie bei einem linearen Regressionsmodell Wahrscheinlichkeiten vorhersagen, indem man Werte für alle unabhängigen Variablen einsetzt. Hier ein Beispiel:
Wahrscheinlichkeit, mit der laut dem geschätzten Modell, eine Frau, die 1200 Euro im Monat verdient und dessen Vater Abitur hat, höchstens einen mittleren Schulabschluss hat: \( P(Y_i \leq j | x_i) = \frac{exp(\alpha_j - x'_i \beta)}{1 + exp(\alpha_j - x'_i \beta)}\) Die entsprechenden Werte wurden dem R-Output entnommen. \(\hat{p}=\frac{exp(2.0906 - (1 \times 0.244 + 1 \times 2.327 + 1200 \times 0.0005))}{1 + exp(2.0906 - (1 \times 0.244 + 1 \times 2.327 + 1200 \times 0.0005))} \approx 0.253\) Die besagte Frau hat also mit einer vorhergesagten Wahrscheinlichkeit von 25,3 % höchstens einen mittleren Schulabschluss. |
|---|
Da die marginalen Effekte keiner so direkten Interpretation wie im linearen Modell zugänglich sind und die vorhergesagten Wahrscheinlichkeiten auch nur spezielle Aussagen ermöglichen, werden oft die sogenannten Odds, Log-Odds (Logits) oder die Oddsratio betrachtet.
Der Quotient \( \frac{P(Y_i \leq j | x_i)}{P(Y_i > j | x_i)}\) wird oft als "Chance" oder englisch "odds" bezeichnet. Odds beschreiben das Verhältnis von Wahrscheinlichkeit zur Gegenwahrscheinlichkeit.
Da die Odds exponentiell sind, bietet es sich an, sie zu logarithmieren, um Zusammenhänge zu linearisieren. So entstehen die Log-Odds, auch Logits genannt:
\[ log \left( \frac{P(Y_i \leq j | x_i)}{P(Y_i > j | x_i)} \right) = log \left( \frac{P(Y_i \leq j | x_i)}{1 - P(Y_i \leq j | x_i)} \right) = \alpha_j - x'_i \beta \]
Die erklärenden Variablen stehen nun in einem linearen Zusammenhang mit den logarithmierten Odds.
Die Oddsratio (OR) setzt die Odds in Relation. Wenn eine Einflussvariable \( x_{i1}\) um eine Einheit auf \( x_{i1} + 1\) erhöht wird, gilt
\[ \frac{\frac{P(Y_i \leq j| x_{i1} + 1)}{P(Y_i > j| x_{i1} + 1)}}{\frac{P(Y_i \leq j| x_{i1})}{P(Y_i > j| x_{i1})}} = exp(\beta_1)\]
Die Odds-Ratio hängt nicht von einer einzelnen Kategorie j ab, sondern nur von den Differenzen in den Kovariaten. Eine wichtige Annahme des kumulativen Logit-Modells ist, dass die Beziehung zwischen jeder möglichen Kombination an Stufenpaaren der Zielvariablen gleich ist. Deswegen kann der Effekt einer erklärenden Variablen durch einen globalen \(\beta\)-Koeffizienten dargestellt werden. Dieser Effekt gilt dann für jeden Stufenwechsel zwischen den Ausprägungen der Zielvariable und ändert sich auch nicht, wenn Kategorien zusammengefasst werden. Daher wird das Modell auch "Proportional Odds"-Modell genannt. Die Annahme ist bekannt unter „proportional Odds“- oder „equal slopes"-Annahme.
Bei einer Odds-Ratio (also \( exp(\beta) \) ), die größer als eins ist, hat die Einflussvariable einen positiven Effekt auf die abhängige Variable, da die Chance \( \frac{P(Y_i \leq j | x_i)}{P(Y_i > j | x_i)}\) größer wird, wenn die Einflussvariable um eine Einheit erhöht wird. Im Gegenzug hat die Variablen einen negativen Einfluss bei einer Odds-Ratio kleiner als eins. Wenn die Odds-Ratio gleich eins ist, hat die Variable keinen Einfluss, weil die Chance/Odds \( \frac{P(Y_i \leq j | x_i)}{P(Y_i > j | x_i)}\) gleich bleibt.
Oddsratio beispielhaft für die Variable Nettoeinkommen: OR: \( \frac{odds(NETTO_i + 1)}{odds(NETTO_i)} = exp(\beta_{NETTO}) = exp(0.000506) = 1.000506 \) . Die Chance, einen höheren Schulabschluss zu haben, steigt um den Faktor 1.000506, wenn man 1 € pro Monat mehr verdient. |
|---|
Die proportional odds ratios werden sehr ähnlich wie im binären logistischen Modell interpretiert (siehe Logistische Regression (Logit-Modell)).
Die Chance bsp. für die Kategorie ABI vs. die zusammengefassten Kategorien MITTEL/HAUPT steigt/sinkt um den Faktor \( exp(\beta)\), falls die erklärende Variable x um eine Einheit erhöht wird (ceteris paribus). Wegen der proportional odds Annahme gilt der gleiche Zusammenhang auch für die zusammengefassten Kategorien ABI/MITTEL vs. HAUPT.
Erhöht man eine Dummy Variable um eine Einheit, setzt man sie von 0 auf 1. Dabei werden die Ergebnisse immer im Vergleich zu Referenzkategorie (des Dummies) interpretiert. Im Beispiel heißt das, dass die Chance auf einen höheren Schulabschluss für Frauen \( e^{0.244}=1.28\) mal höher ist als bei Männern.
Kategoriale Variablen werden ähnlich wie Dummy Variablen behandelt. Zu beachten ist jedoch, dass sie immer in Relation zu Referenzkategorie interpretiert werden müssen. Im Beispiel ist die Chance auf einen höheren Schulabschluss, wenn der Schulabschluss des Vaters das Abitur ist, um den Faktor \( e^{2.327}=10.24 \) höher als wenn der Vater einen Hauptschulabschluss hat.
Interpretation der Schwellenwerte
Die Schwellenwerte \(\alpha_j\) sind Konstanten, die für die Kategorien (außer der letzten) der Zielvariable geschätzt werden müssen. Bei der linearen Regression entspricht das arithmetische Mittel dem Schätzer für das Intercept, falls keine Einflussvariablen aufgenommen werden. Vom Prinzip her ähnlich, entsprechen beim kumulativen Logitmodell die geschätzten Schwellenwertparameter der linken Seite der Regressionsgleichung den Sprungstellen der empirischen Verteilungsfunktion von Y, wenn für alle Einflussvariablen \(x_i = 0 \) gilt. Im Fall mit Einflussvariablen sind die \(\hat{\alpha}_j\) dann die Sprungstellen der bedingten empirischen Verteilungsfunktion von Y.
Man kann die Schwellenwerte im Sinne der Skala der latenten Werte \(y^*\) interpretieren. Wenn die Schwellenwerte den gleichen Abstand haben, so kann dieser Argument für eine metrische Behandlung durch ein lineares Modell genutzt werden.
Interpretation bei sequentiellen Modellen
Die Interpretation der \(\beta\)-Koeffizienten im sequentiellen Modell unterscheidet sich stark von der Interpretation im kumulativen Modell. Im sequentiellen Modell werden sie wie im binären Logit-Modell interpretiert, nur in Bezug auf die jeweils höhere Ausprägung. Der Koeffizient \(\beta_1\) sagt zum Beispiel aus, um wie viel sich die Chance, in eine niedrigere Kategorie von \(Y\) zu fallen, erhöht, wenn man die Variable \(X_1\) um eine Einheit erhöht.
Modellselektion
Das Thema der Modellselektion ist allgegenwärtig in der Regressionsanalyse. Dennoch gibt es keine absoluten, objektiven Kriterien, anhand derer entschieden werden kann, ob das eine oder das andere Modell gewählt werden sollte. Vielmehr existieren viele verschiedene Verfahren, die versuchen, zwischen möglichst viel Erklärungsgehalt des Modells und möglichst wenig Komplexität (siehe dazu Ockhams Rasiermesser) abzuwägen.
Nimmt man zu viele erklärende Variablen auf, läuft man Gefahr, das Modell zu "overfitten" (überanpassen). Ein überangepasstes Modell erklärt die zum Schätzen verwendete abhängige Variable meist sehr gut, schneidet jedoch in der Vorhersage von Daten außerhalb der verwendeten Stichprobe häufig schlecht ab. Auf der anderen Seite kann ein Modell auch "underfitted" sein, d.h. die aufgenommenen unabhängigen Variablen können die abhängige Variable nur sehr unzureichend erklären.
Eine ausführliche Übersicht über verschiedene Verfahren, Modelle zu selektieren, befindet sich im Artikel über Modellselektion.
AIC (Akaike-Information-Criterion)
Das AIC dient dazu, verschiedene Modellkandidaten zu vergleichen. Dies geschieht anhand der logarithmierten Likelihood, die umso größer ist, je besser das Modell die abhängige Variable erklärt. Um nicht komplexere Modelle als durchweg besser einzustufen, wird neben der log-Likelihood noch die Anzahl der geschätzten Parameter als Strafterm mitaufgenommen. Das AIC versucht somit, ein Modell, das die Daten gut beschreibt, gleichzeitig aber nicht zu komplex ist, zu selektieren.
\[AIC(P)=-2\ln(\hat{L})_P+2P\]
In der Formel steht \(P\) für die Anzahl der im Modell enthaltenen Parameter und \(\hat{L}\) für den Wert der Likelihoodfunktion. Das Modell mit dem kleinsten AIC wird bevorzugt.
Das AIC darf nicht als absolutes Gütemaß verstanden werden. Auch das Modell, welches vom Akaike Kriterium als bestes ausgewiesen wird, kann eine sehr schlechte Anpassung an die Daten aufweisen. Die Anpassung ist lediglich besser als in den Alternativmodellen.
BIC (Bayesian-Information-Criterion)
Das BIC (auch SIC, Schwarz Information Criterion, genannt) ist dem AIC sehr ähnlich. Zur Bewertung der Modellgüte wird der Wert der logarithmierten Likelihood herangezogen. Davon wird als Strafterm die Anzahl der geschätzten Parameter multipliziert mit dem natürlichen Logarithmus der Anzahl der Beobachtungen abgezogen. Im Gegensatz zum Akaike Kriteriuim passt sich der Strafterm an die Größe der Stichprobe an. Schon ab einer Stichprobengröße von acht \((\ln(8)=2,07944>2)\) bestraft das BIC komplexere Modelle stärker als das AIC.
\[BIC(P)=-2\ln(\hat{L})_P+P\ln(n)\]
In der Formel steht \(P\) für die Anzahl der im Modell enthaltenen Parameter und \(\hat{L}\) für den Wert der Likelihoodfunktion. Das Modell mit dem kleinsten BIC wird bevorzugt. Auch für das BIC gilt, dass das Modell mit dem kleinsten Wert des Informationskriteriums eine bessere Anpassung aufweist als die Alternativmodelle. Dennoch kann der Gesamterklärungsgehalt des Modells gering sein.
In der Praxis finden beide Auswahlkriterien Anwendung und werden oft sogar zusammen verwendet. Insgesamt ist das AIC jedoch gebräuchlicher als das BIC.
Modellgüte
Da es sich beim Logit-Modell um ein nicht-lineares Modell handelt, ist das Bestimmtheitsmaß (R²) nicht aussagekräftig. Es muss deshalb auf Alternativen zurückgegriffen werden. Im Folgenden werden drei Möglichkeiten vorgestellt.
Pseudo R²
Das R² basiert auf dem Varianzzerlegungssatz, der besagt, dass sich die Varianz der abhängigen Variablen als die Summe eines Varianzteils, der durch das Regressionsmodell erklärt wird und der Varianz der Residuen (nicht erklärte Varianz) schreiben lässt. Das Bestimmtheitsmaß R² ist der Quotient aus erklärter Varianz und Gesamtvarianz. Als Anteilswert kann das R² Werte zwischen 0 und 1 annehmen. Das R² misst aber nur lineare Zusammenhänge, den es beim Logit-Modell jedoch nicht gibt. Die Definition von „Varianz“ ist im diesem Fall anders. Als Basis dienen hier Vergleiche der Likelihood Funktion \(L\) für das Null- und das vollständige Modell. Das Null-Modell ist das Konstantenmodell, bei dem alle Parameter (also \(\beta_1, ...\beta_P\)) auf Null gesetzt werden. Im Unterschied zu nominalen logistischen Modellen, dessen Null-Modell nur aus dem Intercept besteht, enthält das Null-Modell eines kumulativen Logit-Modells die \(\alpha\)-Schätzwerte (Schwellenwertparameter), die den konstanten Part des Modells darstellen. Das Modell hat folglich keine Erklärungskraft. Das vollständige Modell ist jenes, wie man es vorher spezifiziert hat, einschließlich aller Parameter und Variablen. Die Likelihood gibt dann an, wie wahrscheinlich es ist, dass die vorliegenden Daten erzeugt wurden, wenn das Modell stimmt.
Bekannte „Pseudo R²" sind:
\[\text{McFadden } R^2 = 1 - \frac{ln(L_{voll})}{ln(L_{null})}\]
\[\text{Cox&Snell } R^2 = 1 - \left(\frac{L_{null}}{L_{voll}}\right)^{\frac{2}{n}}\]
\[\text{Nagelkerkes } R^2 = \frac{1 - (\frac{L_{null}}{L_{voll}})^{\frac{2}{n}}}{1 - (L_{null})^{\frac{2}{n}}}\]
Aus den vorliegenden Daten lassen sich folgende Werte für die log Likelihood-Funktionen errechnen (siehe Outputs der Statistikprogramme):
\[ln L_{null} = -2475.44\]
\[ln L_{voll} = -2164.66\]
Hieran lässt sich bereits erkennen, dass das volle Modell wahrscheinlicher die Daten erzeugt hat. Um dies zu bestätigen werden die Pseudo R² nun berechnet:
Berechnung der Pseudo R² im Beispiel: \(\text{McFadden } R^2 = 1 - \frac{-2164.66}{-2475.44} = 0.126 \) \(\text{Cox&Snell } R^2 = 1 - \left(\frac{L_{null}}{L_{voll}}\right)^{\frac{2}{2280}} = 0.238 \) \(\text{Nagelkerkes } R^2 = \frac{1 - \left(\frac{L_{null}}{L_{voll}}\right)^{\frac{2}{2280}}}{1 - (L_{null})^{\frac{2}{2280}} } = 0.269 \) |
|---|
Die Interpretation ist anders als im Kontext eines linearen Zusammenhangs. Man kann nun nicht mehr von einem erklärten Anteil sprechen. Vielmehr entziehen sich die Pseudo R² jeglicher inhaltlicher Interpretation. Es gilt jedoch für alle drei vorgestellten Maße folgende Faustregel:
\(R^2 > 0.2:\) Modellanpassung ist akzeptabel \(R^2 > 0.4:\) Modellanpassung ist gut \(R^2 > 0.5:\) Modellanpassung ist sehr gut |
|---|
Likelihood Ratio Test
Die Likelihood \(L\) ist die Wahrscheinlichkeit, mit den geschätzten \(\beta\)-Koeffizienten die empirisch erhobenen Beobachtungswerte zu erhalten, also die Likelihood des vollen Modells. Der Wert \(- 2 ln L\) bezeichnet die Devianz, welche approximativ \(\chi^2\) (Chi-Quadrat-Verteilung) verteilt ist. Mit Hilfe des Likelihood Ratio Tests kann der empirische \(ln L\)-Wert mit der logarithmierten Likelihood des Null-Modells verglichen werden. Null-Modell heißt in diesem Fall, dass eine Schätzung nur mit den \(\alpha\)s erfolgt, alle anderen Parameter (\(\beta_1,...,\beta_P\)) also auf Null gesetzt werden. Die Devianz des Null-Modells (Null deviance) wird dann mit der Devianz des vollständigen Modells (Residual deviance) verglichen. Je größer die Differenz zwischen den beiden Werten ist, desto mehr Einflusskraft haben die erklärenden Variablen insgesamt.
Die Null-Hypothese lautet:
\[H_{0}: \beta_1 = \beta_2 = ... = \beta_P = 0\]
und ist mit dem F-Test der multiplen linearen Regression vergleichbar. Die absolute Differenz der Devianzen ist ebenfalls \( \chi^2 \) verteilt, so dass der p-Wert 1 minus dem Wert der Verteilungsfunktion der \(\chi^2\)-Verteilung an der Stelle der Devianzdifferenz (Null-Modell - Schätzmodell) beträgt und die Freiheitsgrade gleich der Anzahl der Kovariaten ist.
\[p = 1 - \chi^2_{P-m} (-2(ln L_{null} - ln L_{voll})) \]
Ist der p-Wert kleiner als das vorgegebene Signifikanzniveau, kann die Nullhypothese verworfen werden.
Berechnung des p-Wertes im Beispiel: \(-2[(-2475.44) - (-2164.6)] = 621.68 \) \(\chi^2_4(621.68) = 1\) \(p = 1-1 = 0 \) Zu den gängigen Signifikanzniveaus kann die Nullhypothese, dass das volle Modell keine Erklärungskraft besitzt, abgelehnt werden. |
|---|
Modellannahmen und deren Überprüfung
Parallelitätstest für Linien
Die oben genannte Proportional Odds Annahme kann mit Hilfe eines Parallelitätstest für Linien (Link, S. 21) überprüft werden. D.h. der Test prüft die Annahme, ob die \(\beta\)-Koeffizienten einer erklärenden Variablen wirklich global ins Modell eingehen, also für alle Kategorien der Zielvariable gleich sind. Dafür werden für alle Kategorien der Zielvariable getrennte Regressionen durchgeführt und im Anschluss geprüft, ob alle \(\beta\)-Koeffizienten gleich sind (\(H_0\)). Dabei wird die Log-Likelihood (multipliziert mit -2) der ordinalen Regression mit der Log-Likelihood (multipliziert mit -2) verglichen, die entsteht, wenn keine globalen \(\beta\)-Koeffizienten angenommen werden. Mit Hilfe eines Likelihood-Ratio-Tests kann dann eine Testentscheidung getroffen werden.
\(H_0\) = Alle \(\beta\)-Koeffizienten einer erklärenden Variablen sind gleich. vs. \(A\) = Die \(\beta\)-Koeffizienten einer erklärenden Variablen sind nicht gleich.
Die Differenz der beiden Log-Likelihoods ist asymptotisch \(\chi^2\)-verteilt. Die Differenz der zu schätzenden \(\beta\)-Koeffizienten unter \(H_0\) und \(A\) bestimmt die Anzahl der Freiheitsgrade. Die Testentscheidung kann dann wie bekannt beim LR-Test anhand des Chi-Quadratwertes oder des p-Wertes verglichen werden.
Falls die Nullhypothese verworfen werden muss, kann es hilfreich sein, eine andere Verteilungsfunktion für den Link auszuwählen oder eine multinomiale logistische Regression durchzuführen. In einigen Fällen ist die Annahme zwar nicht für alle erklärenden Variablen erfüllt, aber für einige. Dann kann auf Partial Proportional Odds-Modelle zurückgegriffen werden, die für Einflussvariablen, die die Annahme nicht erfüllen, \(\beta\)-Koeffizienten für jeden Stufenwechsel schätzen.
Keine (Multi-)Kollinearität
Die unabhängigen Variablen dürfen untereinander nicht zu stark korrelieren. (Multi-)Kollinearität liegt vor, wenn zwei oder mehr erklärende Variablen eine starke Korrelation untereinander aufweisen (z.B. Brutto- und Nettoeinkommen). Die Überprüfung der Modellannahme unterscheidet sich kaum von anderen Modellen, da die Untersuchung der Multikollinearität unabhängig von der abhängigen Variable ist. Zu beachten ist, dass kategoriale Variablen in einzelne Dummy-Variablen zerlegt werden müssen. Da einige Statistik-Programme keine impliziten Tests auf (Multi-)Kollinearität für ordinale oder logistische Modelle im Allgemeinen anbieten, wird in diesen Fällen empfohlen, die abhängige Variable als metrisch/stetig zu deklarieren und eine einfache lineare Regression durchzuführen, um mögliche Korrelationen zwischen den unabhängigen Variablen mit Standardwerkzeugen wie z.B. dem Variance Inflation Factor (VIF) zu untersuchen.
Komponenten und Begriffe
Die Güte des Modells
1. Gesamtzahl an Beobachtungen:
Die gesamte Anzahl an Beobachtungen im Datensatz entspricht der Anzahl an Zeilen. Diese wird häufig mit n gekennzeichnet. In diesem Datensatz gibt es insgesamt 2280 Beobachtungen.
2. Gelöschte Beobachtungen:
Bei fehlenden Werten in Variablen können Beobachtungen für die Modellanalyse nicht berücksichtigt werden. Im Beispiel sind dies 0 Beobachtungen.
3. Zahl der Beobachtungen:
Hiermit ist die Zahl der Beobachtungen gemeint, die zur Anpassung des Modells genutzt wird. Das bedeutet, dass diese Anzahl sich aus der Differenz der Gesamtzahl an Beobachtungen und den gelöschten Beobachtungen auf Grund von fehlenden Werten in den gewünschten Variablen ergibt. In dem Modell wurden 2280 Beobachtungen genutzt.
6. Pseudo R²
Das geschätzte Modell im Beispiel hat ein McFadden R² von 0.126. Diese Zahl ist nicht direkt interpretierbar (siehe Faustregel oben).
8. Standardfehler des Schätzers:
Da das Logit Modell nicht analytisch lösbar ist, wird der Schätzer numerisch mittels der Maximum-Likelihood Methode ermittelt. Über diese Art von Schätzern können nur asymptotische Aussagen getroffen werden. So entspricht auch der Standardfehler asymptotisch dem Inversen der Fisher-Information.
Schätzergebnisse
9. Abhängige oder endogene Variable:
Im Beispiel ist der Schulabschluss (SCHULABSCHLUSS) die abhängige Variable.
10. Erklärende oder exogene Variable:
Im Beispiel sind das Geschlecht (GESCHL), der Schulabschluss des Vaters (SCHULABSCHLUSS_V) und das Nettoeinkommen (NETTO) die erklärenden Variablen.
11. Geschätzte Parameter:
Bei der ordinalen Regression werden die Schwellenwertparameter (11a), sowie die Regressionskoeffizienten (11b) geschätzt. Die Interpretation ist schwieriger als im linearen Regressionsmodell. In der praktischen Anwendung ist es nicht üblich, die Schwellenwerte zur Interpretation des Modells zu nutzen.
Schätzung im Beispiel: \( log\left( \frac{P(Y_i \leq j | x_i)}{1 - P(Y_i \leq j | x_i)}\right) = \alpha_j - x'_i \beta \) Interpretation der Parameter: Der Schwellenwertparameter (\(\alpha_j\)) zwischen HAUPT und MITTEL entspricht 0.2999, der zwischen MITTEL und ABI 2.0906. Der Steigungsparameter für "NETTO" entspricht bspw. 0.000506. Um diesen sinnvoll zu interpretieren, betrachtet man die Odds Ratio: \(exp(\beta_{NETTO}) = exp(0.000506) = 1.000506 \). D.h. die Chance, einen höheren Schulabschluss zu haben, steigt um den Faktor 1.000506, wenn man 1 € pro Monat mehr verdient. |
|---|
12. Standardabweichung der Schätzung (Standardfehler, \(\widehat{SF}_{\beta_p}\)):
Da die Parameter basierend auf einer Zufallsstichprobe geschätzt werden, unterliegen diese Schätzungen einer gewissen Ungenauigkeit, die durch die Standardabweichung der Schätzung quantifiziert wird. Standardfehler werden genutzt, um statistische Signifikanz zu überprüfen und um Konfidenzintervalle zu bilden.
13. Z-Statistik (empirischer Z-Wert).
Mit Hilfe eines Wald- oder Likelihood-Ratio Tests lässt sich prüfen, ob die Nullhypothese, dass ein Koeffizient gleich 0 ist, abgelehnt werden kann. Wenn dies nicht der Fall sein sollte, ist davon auszugehen, dass die zugehörige Kovariate keinen signifikanten Einfluss auf die abhängige Variable ausübt, d.h. die erklärende Variable ist nicht sinnvoll, um die Eigenschaften der abhängigen Variablen zu erklären.
Hypothese: \(H : \beta_p = 0 \) gegen \(A : \beta_p \neq 0 \)
Teststatistik: \( T = \frac{\hat{\beta_p}}{\widehat{SF}_{\beta_p}}\)
Überprüfen, ob z.B. das Geschlecht einen Einfluss auf den Schulabschluss hat, anhand der Z-Statistik: Die Teststatistik vom Parameter für das Einkommen ist \(T_{GESCHL} = \frac{-0.244}{0.087} \approx -2.81. \) Diese Teststatistik wird mit dem kritischen Wert verglichen: \(|T_{GESCHL}| = 2.81 > 1.96 = z_{1-\frac{\alpha}{2}}\). Schon anhand der Teststatistik kann man erkennen, dass die Nullhypothese \( \beta_{GESCHL} = 0 \) hier abgelehnt werden kann, d.h. dass das Geschlecht einen signifikanten Einfluss auf den Schulabschluss hat. |
|---|
14. p-Wert zur Z-Statistik:
Zusätzlich zur Z-Statistik wird meistens ein p-Wert ausgegeben. Aus einer methodisch-praktisch orientierten Perspektive gibt der p-Wert das kleinste Signifikanzniveau an, zu dem die Nullhypothese \(\beta_p=0\) gerade noch abgelehnt werden kann. Ist also das tatsächliche Signifikanzniveau \( \alpha \), welches vor dem Test gewählt wird, geringer als der p-Wert, so kann die Nullhypothese nicht abgelehnt werden.
Überprüfen, ob z.B. das Geschlecht einen Einfluss auf den Schulabschluss hat, anhand des p-Wertes: Im Beispiel liegt der p-Wert zur Nullhypothese \(\beta_{GESCHL} = 0 \) bei 0.005. Daraus kann man schließen, dass das Geschlecht einen signifikanten Einfluss auf den Schulabschluss hat, und zwar schon bei einem Signifikanzniveau von 0.001. |
|---|
Der p-Wert gibt die Wahrscheinlichkeit an, dass wir unter der Nullhypothese einen Wert der Teststatistik beobachten, der noch stärker in Richtung Ablehnung der Nullhypothese geht. Das heißt er macht eine Aussage über die Wahrscheinlichkeit der Beobachtung der Stichprobe, nicht aber direkt über die Wahrscheinlichkeit der Nullhypothese selbst.
Zum p-Wert gibt es viele Missverständnisse, selbst in veröffentlichter Literatur. Aussagen wie z.B. dass "der p-Wert den Fehler 1. Art wieder gibt" bzw. "die Wahrscheinlichkeit ist, dass unsere Hypothese wahr ist, gegeben, dass der Test abgelehnt wird", sind falsch und sollten in Arbeiten vermieden werden.
Eine gute Quelle für die den richtigen Umgang und ein tieferes Verständnis vom p-Wert gibt es beispielsweise hier.
15. 95%-Konfidenzintervall:
Konfidenzintervalle sind im Allgemeinen eine Möglichkeit, die Genauigkeit der Schätzung zu überprüfen. Ein 95%-Konfidenzintervall ist der Bereich, der im Durchschnitt in 95 von 100 Fällen den tatsächlichen Wert des Parameters einschließt.
Beispielhaftes Konfidenzintervall für den Regressionskoeffizienten der Variable Geschlecht:
[-0.244 - 1.96 * 0.087; 0.244 + 1.96 * 0.087 ] = [-0.41452 ; -0.07348]
Outputs in den verschiedenen Statistikprogrammen
Hier werden die Outputs aus den verschiedenen Statistikprogrammen vorgestellt. Die Outputs einer ordinalen Regression unterscheiden sich teils in den verschiedenen Statistikprogrammen. Sowohl sind die Werte unterschiedlich angeordet, als auch werden teils nicht die gleichen Werte ausgegeben. Einen hilfreichen Überblick über ausführlichere Code-Beispiele für die verschiedenen Statistikprogramme liefert folgende Website (Unterpunkt 'Ordinal Logistic Regression').
Im Folgenden werden die Werte 1-15, wenn vorhanden, an den Output der verschiedenen Statistikprogramme geschrieben, damit die Werte im Output gefunden werden können.
Output in R

Output in Stata

Parameterinterpretation (Odds-Ratios)
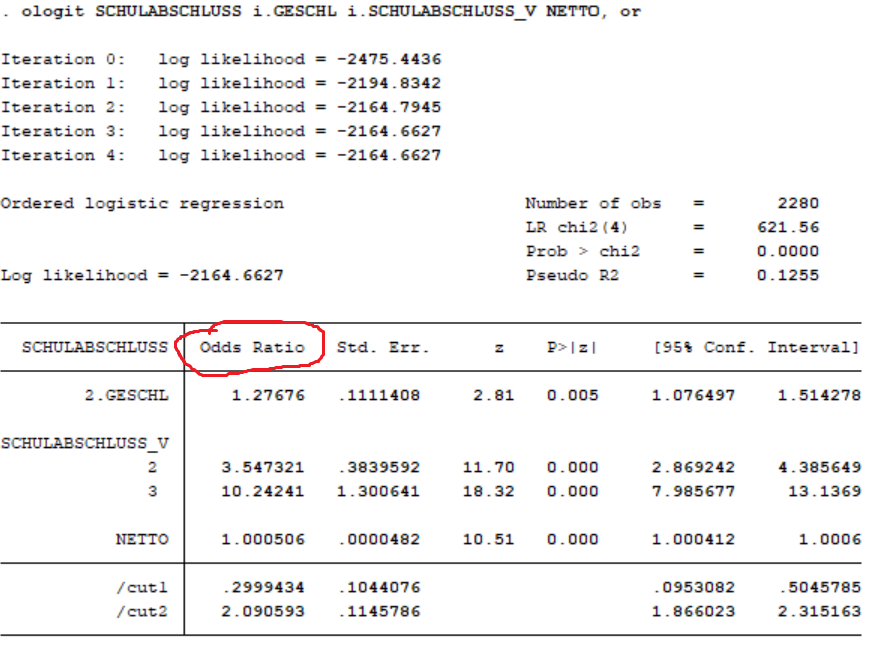
Output in SPSS
Das kumulative Logit-Modell wird in SPSS über den Pfad Analysieren → Regression → Ordinal... durchgeführt. Für die Parameterinterpretation müssen die Odds Ratios händisch ausgerechnet werden (\(exp(\beta) \)).
Achtung: SPSS hat im Gegensatz zu den anderen Statistikprogrammen bei den Faktorvariablen GESCHL und SCHULABSCHLUSS_V eine andere Referenzkategorie gewählt. Entweder muss dies bei der Interpretation beachtet werden oder die Variablen müssen vorher transformiert werden. Hier wurden GESCHL (3 - GESCHL) und SCHULABSCHLUSS_V (4 - SCHULABSCHLUSS_V) transformiert, um die Ergebnisse analog interpretieren zu können.
Sie erhalten unter anderem diesen Output:


Output in SAS
Sie erhalten unter anderem diesen Output:



Anmerkung: SAS gibt statt den Schwellenwerten Intercepts aus, diese sind wie die Schwellenwerte nur mit negativem Vorzeichen.
- Keine Stichwörter
