Seitenhistorie

Die Varianzanalyse oder ANOVA (von analysis of variance) ist ein Verfahren, welches auf Gruppenunterschiede testet. Bei der ANOVA wird versucht, die Gesamtvarianz der abhängigen, metrischen Variable zu zerlegen, daher kommt auch der Name "Varianzanalyse". Dabei wird ein (möglichst großer) Teil der Varianz durch die unabhängigen Faktoren erklärt (Varianz zwischen den Gruppen), während die restliche, nicht erklärbare Varianz als Zufallsprozess aufgefasst wird (Varianz innerhalb der Gruppen). In ihrer einfachsten Form, der einfaktoriellen Varianzanalyse, ist sie als Verallgemeinerung des zwei-Stichproben t-Tests auf Mehr-Gruppen-Vergleiche darstellbar. Natürlich könnte man für alle möglichen Gruppenvergleiche auch paarweise t-Tests durchführen (führt zur Alphafehler-Kumulierung, häufig auch \(\alpha\)-Fehler-Inflation, siehe Artikel über multiples Testen), die . Die Varianzanalyse bietet jedoch mehrere Vorteile. So kann getestet werden, ob ein Faktor als ganzes insgesamt (also über alle Ausprägungen)  einen Erklärungsgehalt besitzt, und es existieren effiziente Testverfahren für multiple Vergleiche (siehe Artikel über multiples Testen). Außerdem bietet sie eine etwas effizientere Schätzung, wenn man davon ausgeht, dass die Varianzen in den Gruppen gleich sind (Varianzhomogenität), da so nur ein Varianzparameter geschätzt werden muss.

Inhaltsverzeichnis

Einfaktorielle Varianzanalyse

Zunächst wird der einfachste Fall, die einfaktorielle Varianzanalyse, behandelt. Getestet werden soll, ob es Mittelwertunterschiede zwischen mindestens drei unabhängigen Stichproben gibt, dabei entspricht der Gesamt-Stichprobenumfang der Summe der Teil-Stichprobenumfänge. Die abhängige Variable muss dabei metrisch skaliert sein (z.B. Körpergröße). Die kategoriale Variable mit \(I\) Kategorien (Ausprägungen), die die Gesamt-Stichprobe in \(I\) unabhängige Teil-Stichproben teilt, nennt man Faktor. Die einzelnen Kategorien (Ausprägungen) eines Faktors werden Faktorstufen genannt. Wenn nur der Einfluss von einem Faktor gemessen werden soll, spricht man von der einfaktoriellen Varianzanalyse. Die zu testende Nullhypothese lautet

$$H_0: \mu_1=\mu_2=... =\mu_I$$

In Worten: Es gibt keine Mittelwertunterschiede zwischen den \(I\) Faktorstufen.

Die Alternativhypothese lautet:

$$H_1: \exists i,j: \ \mu_i \neq \mu_j  $$\mbox{ für mindestens ein i und j} $$

In Worten: Es gibt zwischen mindestens zwei Mittelwerten einen signifikanten Unterschied.

Wie bei jeder statistischen Auswertung empfiehlt sich zunächst eine deskriptive Analyse durchzuführen, um sich einen Überblick über die Daten zu verschaffen. Hierfür eignet sich die Ausgabe der Mittelwerte und Standardabweichungen in den einzelnen Gruppen. Um weitere Einblicke über die Verteilung der Daten in den einzelnen Gruppen zu erlangen, eignen sich graphische Methoden, wie Boxplots und Balkendiagramme der Mittelwerte mit Standardfehlern oder Konfidenzintervallen (bzgl. des Mittelwerts).

Neben der einfachen einfaktoriellen Varianzanalyse existieren noch eine Vielzahl von Erweiterungen und Generalisierungen, auf welche später noch eingegangen wird.

Annahmen:

Für die Gültigkeit der statistischen Tests wird von 3 zentralen Annahmen ausgegangen:

1. Normalverteilte Residuen: Die Fehlerterme sind normalverteilt, d.h. \(\epsilon \sim N(0,\sigma^2)\).
2. Varianzhomogenität: Die Fehlertermvarianz \(\sigma^2\) wird über alle Gruppen gleich angenommen (Homoskedastizitätsannahme).
3. Die Stichproben sind unabhängig.

Die erste Annahme lässt sich grafisch mit Hilfe eines QQ-Plot prüfen. Ein häufiger Fehler, der gemacht wird, ist, die Werte der abhängigen Variablen selber zu verwenden (\(y_i\)), statt die der Residuen (\(\epsilon_i\)). Alternativ kann man die Residuen auch mit einem Test auf Normalverteilung (z.B. Kolmogorov-Smirnov-Test oder Shapiro-Wilk) überprüfen, jedoch ist dies nur begrenzt sinnvoll (siehe folgende Diskussion zu diesem Thema). Solange es zu keinen gravierenden Abweichungen von der Normalverteilung kommt, ist diese Annahme insbesondere bei großen Fallzahlen aufgrund des zentralen Grenzwertsatzes bei kleineren Abweichungen vom Idealfall tolerabel.

Die zweite Annahme kann mit Hilfe des Levene-Test überprüft werden (wobei dieser eine relativ geringe Power besitzt). Auch hier gilt, dass die Varianzanalyse relativ robust gegenüber leichten bis mittleren Verletzungen dieser Annahme ist, wie viele Simulationen gezeigt haben.

Falls die obigen Annahmen erheblich verletzt sind, empfiehlt es sich, zunächst eine Transformation der abhängigen Variablen vorzunehmen. Sinnvoll ist insbesondere die Logarithmus-Transformation, da viele Variablen, wie z.B. das Einkommen, eher auf einer multiplikativen Skala statt einer additiven Skala Sinn ergeben. Weitere Transformationen sind die Wurzeltransformation oder die Box-Cox-Transformation. Wenn dies immer noch nicht zum Erfolg führt, gibt es nichtparametrische, bzw. robuste Alternativen (siehe unten).

Grundlegende Testidee:

Gegeben sei \(x_{ij}\) die j-te Beobachtung der i-ten unabhängigen Stichprobe und \(\overline{x}\) der Mittelwert der Gesamtstichprobe, sowie \(\overline{x}_{i}\) der Mittelwert der i-ten Gruppe (Teilstichprobe). Daraus folgt:

$$x_{ij}=\overline{x}+\underbrace{(\overline{x}_{i}-\overline{x})}_{\text{Abweichung Gruppenmittel vom Gesamtmittel}} + \underbrace{(x_{ij}-\overline{x_{i}})}_{\text{Abweichung Beobachtung vom Gruppenmittel}}.$$

Unter der \(H_{0}\) wird die Abweichung der Gruppenmittel zum Gesamtmittel klein sein im Vergleich zur Abweichung der Beobachtungen zum Gruppenmittel. Eine hohe Abweichung der Gruppenmittel zum Gesamtmittel im Vergleich zur Abweichung der Beobachtungen zum Gruppenmittel spricht dagegen für die \(H_{1}\).

Formal folgt daraus, die folgende Teststatistik:

$$F_{0,\alpha}:=\frac{\frac{1}{I-1}SSA}{\frac{1}{n-I}SSE}=\frac{\frac{1}{I-1}J\sum_{i=1}^{J}(\overline{x}_{i}-\overline{x})^{2}}{\frac{1}{n-I}\sum_{i=1}^{I}\sum_{j}^{J}(x_{ij}-\overline{x}_{i})^2}$$

• SSA:= Sum of Squared errors of All treatment, (sample) means vs. grand mean  (quadratische Abweichung der Mittelwerte vom Gesamtmittelwert der Gruppen).
• SSE:= Sum of Squared Errors of all observation vs. respective sample means (gesamte Abweichung von den Mittelwerten in den Gruppen).
• SST:= Sum of Squared errors Total for all observations vs. grand mean = SSA+SSE

Je weiter die Mittelwerte der einzelnen Faktorstufen vom Gesamtmittelwert abweichen, desto größer wird der Wert für SSA im Vergleich zum Wert für SSE. Bei Gültigkeit der \(H_{0}\) sollte der Quotient \(\frac{SSA}{SSE}\) nahe bei Null liegen. Je größer SSA wird - und somit auch \(\frac{SSA}{SSE}\) - desto unwahrscheinlicher ist die Gültigkeit der \(H_{0}\). Bei zu großen Werten von F wird \(H_{0}\) zu Gunsten der \(H_{1}\) verworfen.

Post-Hoc-Tests:

Wird die \(H_{0}\) der einfaktoriellen Varianzanalyse verworfen, bedeutet dies, dass es einen Mittelwertunterschied zwischen mindestens zwei Gruppen gibt. Da es sich bei dem F-Test der Varianzanalyse um einen globalen Test (Omnibustest) handelt, enthält er keine Information darüber, zwischen welchen zwei, der \(I\) Gruppen, ein Mittelwertunterschied vorliegt. Um zu überprüfen welche zwei Gruppenmittelwerte der \(I\) Gruppen sich signifikant voneinander unterscheiden, werden sogenannte Post-Hoc-Tests verwendet. Ein naives Vorgehen wäre die paarweise Überprüfung mit Hilfe von t-Tests, da es hierbei aber zur bereits erwähnten Alphafehler-Kumulierung kommt, gibt es speziell entwickelte Testverfahren. Eine sehr gute Übersicht über die gängigen Post-Hoc-Tests findet man hier.

Beispiel:

Die einfaktorielle Varianzanalyse wird jetzt anhand eines Beispiels genauer erläutert. Es soll mit Hilfe einer Umfrage unter Studenten der wirtschaftswissenschaftlichen Fakultät der FU-Berlin überprüft werden, ob es signifikante Körpergrößenunterschiede zwischen Studenten aus Berlin, aus einem anderen Bundesland und dem Ausland gibt. Die abhängige metrischen Variable ist hierbei die Körpergröße und die Herkunft (mit den drei Ausprägungen, Faktorstufen) fungiert als Faktorvariable. In diesem Beispiel wird davon ausgegangen, dass alle Annahmen der ANOVA erfüllt sind.

Nach Durchführung der einfaktoriellen Varianzanalyse mit SPSS erhalten wir folgende Ausgabe:

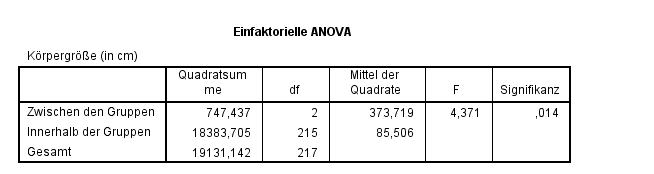
In der Ausgabe finden wir Informationen zu den Quadratsummen zwischen und innerhalb der Gruppen. Wie aus der Beschreibung der grundlegenden Testidee ersichtlich wurde, sprechen hohe Abweichungen zwischen den Gruppen im Verhältnis zu kleinen Abweichungen innerhalb der Gruppen für die \(H_{1}\). Die Berechnung des Quotienten \(373.719/85.506\) ergibt den Wert der Teststatistik \(F=4.371\). Um die Testentscheidung zu treffen gibt uns SPSS außerdem den p-Wert unter dem Namen "Signifikanz" aus. Da der p-Wert mit \(0.014 < 0.05\) ist, lehnen wir die \(H_{0}\) ab. Inhaltlich bedeutet dies, dass es zu einem Signifikanzniveau von 5% einen signifikanten Körpergrößenunterschied (Mittelwertunterschied) zwischen den Studierenden mit unterschiedlicher Herkunft gibt. Um herauszufinden, zwischen welchen Mittelwertpaaren es signifikante Unterschiede gibt, wird ein Post-Hoc-Test (der Least significant difference test (LSD)) verwendet. 

Nach Durchführung des Post-Hoc-Tests mit SPSS erhalten wir folgende Ausgabe:

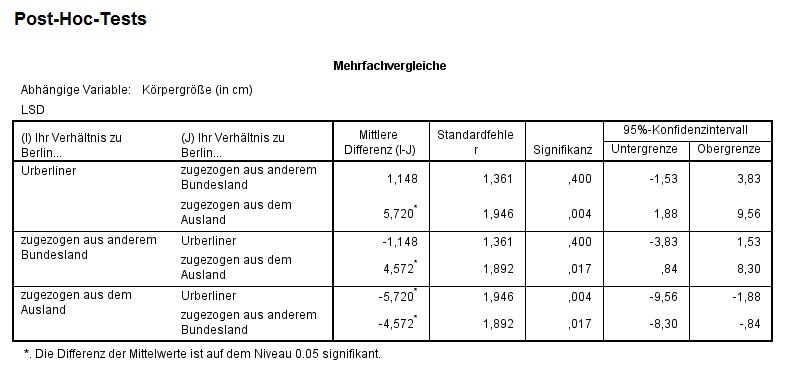
Wie aus der Abbildung ersichtlich wird, werden alle Gruppen paarweise miteinander verglichen (Urberliner mit zugezogen aus anderem Bundesland, Urberliner mit zugezogen aus dem Ausland, usw.). Der Output zeigt die Differenz zwischen den Mittelwerten der Gruppen, den Standardfehler, den p-Wert (unter Signifikanz) und das 95%-Konfidenzintervall. Inhaltlich kann gesagt werden, dass es zu einem Signifikanzniveau von 5% signifikante Größenunterschiede zwischen Urberlinern und aus dem Ausland zugezogenen Studenten (\(p-Wert=0.004<0.05\)), sowie zwischen aus einem anderen Bundesland und aus dem Ausland zugezogenen Studenten (\(p-Wert=0.017<0.05\)) gibt. Die Testentscheidung kann natürlich auch mit Hilfe des 95%-Konfidenzintervalls getroffen werden. Beim Blick auf das Konfidenzintervall für die Mittlere Differenz zwischen Urberlinern und Studenten, die aus dem Ausland zugezogen sind, fällt auf, dass dieses die 0 nicht beinhaltet \([ 1.88;9.56 ] \). Die inhaltliche Interpretation entspricht der Interpretation des Testergebnisses.

Kruskal-Wallis-Test als nichtparametrische Alternative

Wenn die Normalverteilungsannahme der einfaktoriellen ANOVA nicht erfüllt ist, kann auf den Kruskal-Wallis Test als nichtparametrische Alternative zurückgegriffen werden. Der Kruskal-Wallis-Test kann als Verallgemeinerung des, für den 2 Stichprobenfall verwendeten Mann-Whitney-U-Tests verstanden werden. Betrachtet werden, wie beim Mann-Whitney-U-Test, nicht die konkreten Realisierungen \(x_{ij}\), sondern die entsprechenden Ränge \(R_{ij}\). Die zu testende Nullhypothese lautet: \(H_{0}:\) Die \(I\) Stichproben entstammen der gleichen Grundgesamtheit.

Grundlegende Testidee:

Um die Testentscheidung zu treffen, entweder die \(H_{0}\) abzulehnen oder beizubehalten, wird die Teststatistik \(H\) berechnet. Dafür werden alle Stichproben vereinigt und allen \(n\) Realisierungen \(x_{ij}\), Ränge \(R_{ij}\) zugewiesen. Anschließend folgt die Berechnung der Rangsummen \(R_{i}\) für die einzelnen Gruppen. Wenn keine Bindungen vorliegen, also keine Realisierungen doppelt vorkommen, ergibt sich die folgende Teststatistik:

$$H= \tfrac{12}{n(n+1)}\sum_hi\tfrac{SR_h^2i^2}{n_h}-3(n+1)$$

Wenn Bindungen vorliegen, muss die folgende Teststatistik verwendet werden:

$$H= \frac{\tfrac{12}{n(n+1)}\sum_hi\tfrac{SR_h^2i^2}{n_h}-3(n+1)}{1-\tfrac{1}{(n^3-n)} \sum t_{r(i)}^3 - t_{r(i)}},$$

\(t_{r(i)}\) beschreibt die Anzahl der Beobachtungen mit Rang \(i\). Die Teststatistik \(H\) ist unter der \(H_{0}\) Chi-Quadrat-verteilt mit Freiheitsgraden \(Df=kI-1\), wobei \(kI\) für die Anzahl der Gruppen steht. Wie bei der zuvor beschriebenen einfaktoriellen ANOVA ist es sinnvoll, Post-hoc-Tests durchzuführen, um zu untersuchen, zwischen welchen Gruppen signifikante Unterschiede vorliegen.

Beispiel:

Als einführendes Beispiel dient uns das bereits beschriebene Testszenario. Es soll herausgefunden werden, ob die Körpergrößen der Studenten der Gruppen Berliner, zugezogen aus dem Ausland und zugezogen aus einem anderen Bundesland der gleichen Grundgesamtheit entstammen. Nach Auswahl des Kruskal-Wallis-Tests bei SPSS erhalten wir den folgenden Output.

In dem Output kann die \(H_{0}\) abgelesen werden. Es wird außerdem zur Überprüfung angezeigt, welchen Test wir gewählt haben (den Kruskal-Wallis-Test bei unabhängigen Stichproben). Außerdem wird unter "Sig." der p-Wert ausgegeben und die Testentscheidung verbalisiert. Da der p-Wert mit 0.007 kleiner ist als 5%, wird die \(H_{0}\) zu einem Signifikanzniveau von 5% verworfen. Dementsprechend ist die Verteilung der Körpergröße nicht über die Studentengruppen hinweg identisch.

Erweiterungen

Neben der bisher vorgestellten einfaktoriellen ANOVA und ihrem nichtparametischen nichtparametrischen Pendant, dem Kruskal-Wallis Test, gibt es noch eine Reihe an Erweiterungen. Im Folgenden wird daher auf einige, häufig verwendet Erweiterungen kurz eingegangen.

Mehrfaktorielle ANOVA

Wie die einfaktorielle ANOVA, dient auch die mehrfaktorielle ANOVA dem Zweck, Mittelwertunterschiede zwischen unabhängigen Gruppen auf Signifikanz zu testen. Der Unterschied besteht darin, dass sich die unabhängigen Gruppen nicht aus einem Faktor bilden, wie im einfaktoriellen Fall, sondern aus mehreren. Was dies genau bedeutet, lässt sich einfach anhand eines konkreten Beispiels verdeutlichen. Im vorherigen Beispiel kann es sein, dass die Körpergrößenunterschiede eher auf das Geschlecht und weniger auf die Herkunft zurückzuführen sind. Um für das Geschlecht zu "kontrollieren", ist es sinnvoll, den Faktor Geschlecht mit in die Analyse aufzunehmen. Daraus ergeben sich jetzt sechs unabhängige Gruppen (3 Herkunftskategorien mal 2 Geschlechtskategorien). In diesem Fall spricht man auch von einem \(3 \times 2\) Design. 

Die grundlegende Testidee bleibt die gleiche. Es wird probiert, die Varianz der abhängigen Variable (z.B. Körpergröße) mit Hilfe von mehreren unabhängigen Variablen zu erklären (Herkunft, Geschlecht). Dafür wird erneut die Gesamtvarianz in die "Varianz innerhalb der Gruppen" und die "Varianz zwischen den Gruppen" zerlegt. Im Unterschied zur einfaktoriellen Varianzanalyse wird die Varianz zwischen den Gruppen im mehrfaktoriellen Fall weiter aufgegliedert: In die Varianz der einzelnen Faktoren und in die Varianz der Interaktionen der Faktoren. Anschließend wird erneut die Varianz zwischen den Gruppen mit der Varianz innerhalb der Gruppen verglichen.

Natürlich müssen für die Durchführung der Varianzanalyse erneut eine Reihe von Annahmen überprüft werden. Da diese sich nicht von der einfaktoriellen ANOVA unterscheiden, wird auf eine erneute Auflistung verzichtet. Um festzustellen, welche Gruppen sich signifikant voneinander unterscheiden, können abermals die beschriebenen Post-Hoc-Tests angewendet werden. Zusätzliche ausführliche Informationen zur mehrfaktoriellen Varianzanalyse finden Sie hier im Netz.

Analysis of Covariance (ANCOVA)

Die ANCOVA gehört zu der Modellklasse der generalisierten linearen Modelle und kann als Mischung zwischen einer linearen Regression und einer ANOVA angesehen werden. Ziel ist die Untersuchung einer abhängigen Variable auf Mittelwertunterschiede zwischen den einzelnen Faktorstufen der unabhängigen Variablen, wobei der Effekt von stetigen Kovariaten berücksichtigt wird. Die stetigen Kovariaten sind nicht von primären inhaltlichen Interesse und dienen lediglich als "Kontrollvariablen". Bei der ANCOVA wird die Gesamtvarianz in die Varianz der Kovariate, die Varianz der kategorialen unabhängigen Variablen und die Varianz der Residuen zerlegt. Die ANCOVA kann genutzt werden, um die statistische Power (also das Auffinden von signifikanten Mittelwertunterschieden zwischen den Gruppen, falls welche existieren) der Analyse zu erhöhen. Dies geschieht, indem die Varianz innerhalb der Gruppen minimiert wird. Zum besseren Verständnis ist es hilfreich, die Funktionsweise des F-Tests noch einmal zu verdeutlichen: 

$$F=\frac{\text{Varianz zwischen den Gruppen}}{\text{Varianz innerhalb der Gruppen}}.$$

Wie aus der Formel ersichtlich, wird der F-Test berechnet, indem die Varianz zwischen den Gruppen, durch die Varianz innerhalb der Gruppen dividiert wird. Wenn der Quotient größer als ein kritischer Wert wird, spricht dies für ein signifikantes Testergebnis. Folglich bedeutet dies, dass, wenn die Varianz innerhalb der Gruppen mit Hilfe von Kovariaten besser erklärt werden kann, der Nenner kleiner und der Wert des Quotienten größer wird. Sollten signifikante Unterschiede zwischen den Gruppen vorhanden sein, werden diese besser sichtbar.

Annahmen

Für die Durchführung der ANCOVA müssen die Annahmen der linearen Regression erfüllt sein. Außerdem muss angenommen werden, dass die Steigung der Regressionsgerade der Kovariate zwischen den Gruppen gleich ist (Homogenität der Regressionssteigung).

Multivariate ANOVA (MANOVA)

Im Falle von mehr als zwei abhängigen Variablen kann die Multivariate ANOVA (MANOVA) - eine Erweiterung der ANOVA - verwendet werden. Mit Hilfe der MANOVA kann untersucht werden, ob die unabhängigen Variablen einen signifikanten Einfluss auf die abhängigen Variablen haben. Häufig folgen anschließende Signifikanztests, um die abhängigen Variablen erneut einzeln zu überprüfen. 

Die MANOVA kann leicht anhand des vorherigen Beispiel motiviert werden. In diesem wurde getestet, ob es Körpergrößenunterschiede zwischen den unabhängigen Stichproben gibt. Interessieren daneben noch weitere abhängige Variablen (z.B. das Körpergewicht) können entweder sequentiell mehrere ANOVAs (in diesem Fall zwei) oder die MANOVA durchgeführt werden. Das Problem bei der sequentiellen Durchführung von mehreren ANOVAs besteht darin, dass die Wahrscheinlichkeit die \(H_{0}\) fälschlicherweise zurückzuweisen mit jeder weiteren ANOVA steigt. Bei der MANOVA wird hingegen die simultane Irrtumswahrscheinlichkeit auf dem Alpha-Niveau gehalten.