- Erstellt von Andreas Hicketier, zuletzt geändert von Claudia Baldermann am 19.09.2016
Sie zeigen eine alte Version dieser Seite an. Zeigen Sie die aktuelle Version an.
Unterschiede anzeigen Seitenhistorie anzeigen
« Vorherige Version anzeigen Version 23 Nächste Version anzeigen »
Statistische Analyseverfahren, die mit den Begriffen Cluster- oder Paneldaten in Verbindung stehen, werden in verschiedenen Forschungsdisziplinen mit unterschiedlichen Synonymen bezeichnet. Gängige Bezeichnungen in der Psychologie, Medizin und empirischen Sozialforschung sind zum Beispiel Mehrebenenanalyse (multilevel modeling), Hierarchische lineare Modellierung (hierarchical linear models) und Analyse gemischter Modelle (mixed model analysis). In der Ökonometrie, vor allem in der Längsschnittforschung, ist vorrangig der Begriff der Paneldatenanalyse geprägt. In den meisten Fällen bezieht sich die Bezeichnung auf die Struktur der vorliegenden Daten.
Literaturehinweise
hier vielleicht empfehlungen für Literatur und inteessante Links aus verschiedenen Disziplinen
Datenstruktur
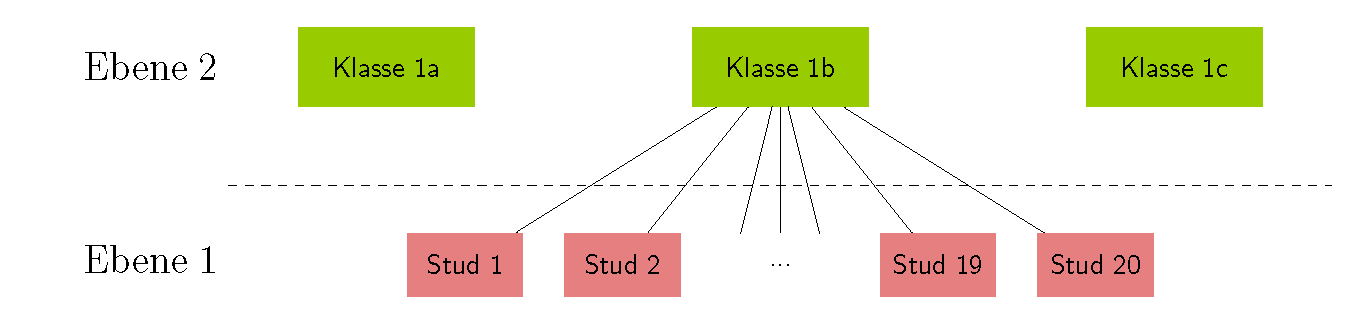
In einem Datensatz können Beobachtungseinheiten in mehreren Ebenen enthalten sein. Ein Beispiel mit zwei Ebenen aus der Bildungsforschung wäre eine Untersuchung des Lernerfolgs von Schülern (Ebene 1) aus verschiedenen Klassen (Ebene 2). Hierbei bilden die Beobachtungen der Schüler die erste Ebene und die Verschiedenen Klassen die zweite Ebene. Es können Charakteristika (Variablen) auf Schülerebene (z.B. Testergebnisse aus Leistungskontrollen, Geschlecht) und auf Klassenebene (z.B. Klassengröße, Eigenschaften des Klassenlehrers) im Datensatz enthalten sein. Die folgene Darstellung zeigt eine schematische Darstellung dieser Datenstruktur. Der Abbildung steht eine Datentabelle gegenüber, die verdeutlicht, wie die Daten orgenisiert sein müssen, um eine Mehrebenenanalyse durchführen zu können.
Fehler beim Ausführen des Makros 'viewxls'
com.atlassian.confluence.macro.MacroExecutionException: com.atlassian.confluence.macro.MacroExecutionException: The viewfile macro is unable to locate the attachment "Beispiel 2 Ebenen.xlsx" on this page
Diese Datenstruktur kann auf Beispiele aus anderen Forschungsdisziplinen übertragen werden: in der Paneldatenanalyse entsprechen die Individuen der Ebene 2 und die Zeitpunkte der Ebene 1; in klinischen Studien mit Patienten aus unterschiedlichen Kliniken entsprechen die Kliniken der zweiten Ebene und die Patienten der ersten Ebene. Das obige Beispiel aus der Bildungsforschung lässt sich auf mehr als zwei Ebenen erweitern. Werden die Schüler zum Beispiel über mehrerer Zeitpunkte beobachtet, kommt eine weitere Ebene hinzu. Die folgende Abbildung verdeutlicht dies

Fehler beim Ausführen des Makros 'viewxls'
com.atlassian.confluence.macro.MacroExecutionException: com.atlassian.confluence.macro.MacroExecutionException: The viewfile macro is unable to locate the attachment "Beispiel 2 Ebenen.xlsx" on this page
Analog zu dieser Erweiterung könnten in der Paneldatenanalyse die Individuen aus unterschiedlichen Regionen stammen. Die Regionen würden in diesem Fall Ebene 3, die Individuen Ebene 2 und die Zeitpunkte Ebene 1 entsprechen. Im Beispiel der Klinischen Studie könnten die Patienten über mehrere Zeitpunkte beobachtet werden, wobei die Kliniken dann Ebene 3, die Patienten Ebene 2 und die Zeitpunkte Ebene 1 entsprächen.
Die Datenstruktur bestimmt die Abhängigkeitsstruktur oder auch Clusterung in den Daten. Als Cluster werden allgemein Beobachtungen bezeichnet, die sich aufgrund von Gemeinsamkeiten ähneln. Im Beispiel wird die Abhängigkeit durch die Klassenzugehörigkeit bestimmt. Es ist zu erwarten, dass die Ergebnisse der Schüler innerhalb einer Klasse sich ähnlicher sind als die Ergebnisse im Vergleich zwischen den Klassen. Dies ist bedingt durch messbare klassenspezifische Faktoren, wie Klassengröße oder Geschlecht Lehrers, aber auch durch nicht messbare Faktoren, wie Zusammengehörigkeitsgefühl oder Beziehung zum Lehrer. Werden die Schüler zusätzlich über verschiedene Zeitpunkte beobachtet, kommt eine zeitliche Abhängigkeit hinzu. Es ist zu erwarten, dass sich die Ergebnisse eines Schülers über die Zeit ähnlicher sind als die Ergebnisse unterschiedlicher Schüler. Dies ist Bedingt durch beobachtbare schülerspezifische Eigenschaften, wie Geschlecht oder sozioökonomische Kennzahlen des Elternhauses, aber auch nicht beobachtbaren Eigenschaften, wie Motivation für das Fach oder Begabung. Diese Abhängigkeit, die durch Zugehörigkeit in den verschieden Ebenen bedingt ist wird allgemein als Intraklassenkorrelation (geläufige Abkürzung ICC) bezeichnet.
Auswertungsmöglichkeiten
Im Beispiel aus der Bildungsforschung könnten die Daten genutzt werden, um Ergebnisse eines Leistungstest mit verschiedenen unabhängigen Variablen zu erklären. Drei mögliche Herangehensweisen werden hier kurz dargestellt.
Aggregieren
Die auf Ebene 1 gemessen Variablen, werden auf Ebene 2 zusammengefasst. Für das obige Beispiel hieße das, dass Mittelwerte über die Schüler innerhalb der einzelnen Klassen gebildet werden. Dieses Vorgehen hat einen massiven Informationsverlust zur Folge und die Stichprobengröße wird auf die Anzahl der in Ebene 2 beobachteten Einheiten reduziert, im Beispiel die Anzahl der beobachteten Schulklassen.
Auswertung auf Individualebene
Die hierarchische Datenstruktur wird ignoriert, und die Daten werden behandelt als wären sie unabhängig. In einer OLS Regression, die Unabhängigkeit der Beobachtungen voraussetzt, könnte das eine fehlerhafte Inferenz zur Folge haben. Die Standardfehler würden tendenziell unterschätzt werden, was die Wahrscheinlichkeit erhöht Effekte fälschlicherweise als signifikant anzunehmen.
Mehrebenenanalyse
Verschiedene Ebenen in ein Modell integriert. Die abhängige Variable auf individualebene, individuenspezifische erklärende, Kontextvariablen auf den verschiedenen Ebenen.
$$Y_{ij} = \underbrace{\alpha_0+ \alpha_1 X_{ij} + \gamma_1 Z_j + \gamma_{11}Z_jX_{ij}}_{fester\,\, Teil} + \underbrace{u_{0j} + u_{1j} X_{ij}+ e_{ij}}_{zufälliger\,\, Teil}$$.
Möglichkeit 2 : Ein bisschen über intuition hinaus. mit Modellgleichung und erklärung zu einzelnen komponenten.
- Keine Stichwörter