Das multiple lineare Regressionsmodell, in seiner allgemeinen Form mit \(P\) Kovariaten, wird folgendermaßen beschrieben:
\[ Y_{i} = \beta_0 + \beta_1 \cdot x_{1i} + \beta_2 \cdot x_{2i} + \ldots + \beta_P \cdot x_{Pi} + \epsilon_i \qquad (i=1,\ldots ,n) \]
Dabei werden folgende Annahme über den Fehlerterm \(\epsilon_i\) getroffen:
| \(\epsilon_{1}, \ldots, \epsilon_{n}\) | sind normalverteilt mit Mittelwert 0 (\(E(\epsilon_{i}) = 0\)) und konstanter Varianz (\(V(\epsilon_{i}) = \sigma^{2}\); Homoskedastizität). (Die Normalverteilungsannahme wird benötigt, um Standard-Tests im Regressionsmodell durchführen zu können, für die Schätzung an sich ist sie nicht erforderlich) |
| \(\epsilon_{1}, \ldots, \epsilon_{n}\) | sind unabhängig |
| \( \epsilon_{i}\) und \(X_{i,p} \:(p=1, \ldots, P) \) | sind unkorreliert |
Annahmen des multiplen linearen Regressionsmodells
Etwas weniger technisch werden in der folgenden Tabelle alle Annahmen, die für das multiple lineare Regressionsmodell (inklusive der Annahmen über den Fehlerterm \(\epsilon_i\)) getroffen werden, dargestellt. In dem nachfolgenden Absatz wird erklärt, wie festgestellt werden kann, ob eine dieser Annahmen verletzt ist.
| Annahme | Was bedeutet das wirklich? | Wann wird die Annahme wahrscheinlich verletzt? | Warum is das ein Problem? |
|---|---|---|---|
| Linearität | Lineare Abhängigkeit zwischen den erklärenden Variablen und der Zielvariable | Schätzwerte der Koeffizienten sind verzerrt, falls der Zusammenhang nichtlinear ist. | |
| Erwartungswert der Störgröße gleich Null | Die Beobachtungen der abhängigen Variable y weichen nicht systematisch von der Regressionsgeraden ab, sondern streuen zufällig darum. | Klar voneinander abgegrenzte Untergruppen in den Daten können dieses Problem verursachen (Männer vs Frauen). | Verzerrung der Schätzung von \(\beta_{0}\) |
Unabhängigkeit der Fehlerterme | verschiedene Beobachtungseinheiten beinflussen sich nicht gegenseitig | Abhängigkeit der Beobachtungen tritt häufig in der Zeitreihenanalyse auf (Temperaturen in Sommer vs. Winter) | Verzerrung bei der Ermittlung der Standardfehler und Konfidenzintervalle; daraus folgt Ineffizienz der Schätzung |
| Die Varianz des Fehlerterms darf nicht von unabhängigen Variablen oder der Beobachtungsreihenfolge abhängig sein, somit sollte die Varianz konstant für alle Beobachtungseinheiten sein | Klar voneinander abgegrenzte Untergruppen in den Daten können dieses Problem verursachen (Männer vs Frauen). | Konfidenzintervalle und Hypothesentests sind nicht verlässlich, da die Standardfehler der Regressionskoeffizienten verfälscht berechnet werden. Die geschätzten Koeffizienten sind nicht mehr BLUE (nicht mehr effizient). | |
Residuen normalverteilt | Die Fehlerterme folgen eine Normalverteilung | Das passiert, wenn die berechnete Linearkombination der Kovariaten die Verteilung der unabhängigen Variable nicht gut genug abbilden | Konfidenzintervalle und Hypothesentests sind ungültig |
| Die unabhängigen Variablen dürfen untereinander nicht zu stark korrelieren. | (Multi) Kollinearität liegt vor, wenn zwei oder mehr erklärende Variablen eine starke Korrelation untereinander aufweisen (z.B. Brutto- und Nettoeinkommen) | Schätzungen der Regressionsparameter werden unzuverlässig; Redundanz in den Daten durch Überschneidung der Streuung in den unabhängigen Variablen => weniger Aussagekraft durch das Modell; möglicherweise werden Koeffizienten insignifikant, obwohl sie Erklärungsgehalt bieten | |
| \(Cov(X,\epsilon)=0\) | Unkorreliertheit von unabhängigen Variablen und Störterm | Diese Annahme wird beispielsweise verletzt, wenn nicht alle für das Modell relevanten Kovariate aufgenommen werden (können) und diese mit enthaltenen Variablen korreliert sind | Die geschätzten Koeffizienten der endogenen Variablen sind verzerrt. OLS (kleinste Quadrate Methode) berechnet stets die Parameter, die die Fehler und unabhängigen Variablen unkorreliert erscheinen lassen. |
Überprüfung der Annahmen des multiplen linearen Regressionsmodells:
Die Annahmen, welche in der vorherigen Tabelle beschrieben worden sind, sollten vor einer multiplen linearen Regressionsanalyse überprüft werden.
linearer Zusammenhang
Zunächst sollte untersucht werden, ob zwischen den metrischen unabhängigen Variablen und der abhängigen Variable überhaupt ein linearer Zusammenhang besteht. Dies lässt sich grafisch anhand von Streudiagrammen überprüfen.
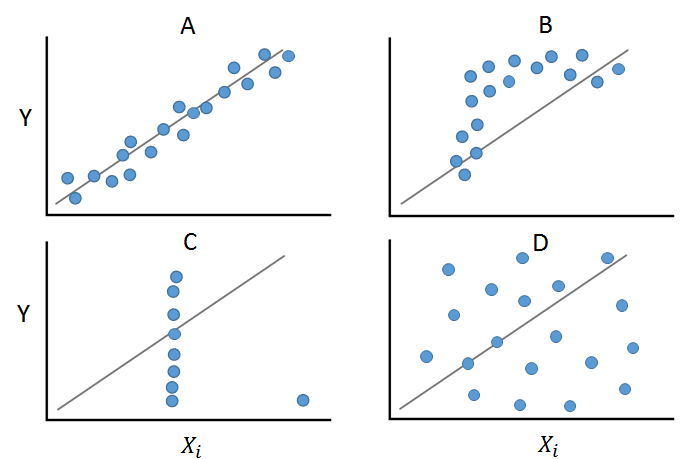
Es ist sehr hilfreich sich die jeweiligen Streudiagramme anzuschauen, da der Korrelationskoeffizient bei beispielsweise extremen Ausreißern oder einem nichtlinearen Zusammenhang zwischen zwei Variablen irreführende Werte annimmt. Das Plotten der Daten vor dem Berechnen eines Korrelationskoeffizienten ermöglicht, die lineare Beziehung zu überprüfen und mögliche Ausreißer zu identifizieren. Der Fall (A) zeigt starke positive Korrelation (= steigende Gerade). Fall (B) hingegen verbildlicht einen Fall in dem ein linearer Zusammenhang als Annahme unpassend ist. Fall (C) veranschaulicht ein Beispiel für eine sehr starke lineare Beziehung mit einem extremen Ausreißer. In diesem Fall wird wegen des Ausreißers ein geringerer Korrelationskoeffizient ausgegeben, obwohl für diese Daten die Annahme eines linearen Zusammenhangs (eventuell nach Ausschluss des Ausreißers) sehr sinnvoll ist. (D) zeigt ein Beispiel in dem keine Korrelation zwischen den Variablen zu beobachten ist und die Annahme eines linearen Zusammenhangs nicht sinnvoll erscheint.
Eine andere Möglichkeit zur Überprüfung des linearen Zusammenhangs ist die Benutzung von Partial Residual Plots. Diese werden verwendet, falls es mehr als eine unabhängige Variable gibt. Gewöhnliche Streudiagramme bilden immer den Zusammenhang zweier metrischer Variablen ab, ohne dass der Einfluss anderer, sich im Modell befindlicher Variablen beachtet wird. Bei Partial Residual Plots wird also das Verhältnis zwischen einer unabhängigen und der abhängigen Variable unter Berücksichtigung der anderen im Modell enthaltenen Kovariaten abgebildet. Wie im Streudiagramm wird auf der Abszisse die unabhängige Variable, auf der Ordinate hingegen die sogenannte Komponente zuzüglich der Residuen aus dem geschätzen Modell abgetragen. Die Komponente entspricht \(\hat{\beta}_{i}\cdot X_{i}\), berücksichtigt also durch den geschätzten Beta-Wert der i-ten Variable den Einfluss der anderen Kovariate im Modell. Ein linearer Zusammenhang wird auf dem Schaubild in Form einer roten Geraden (Steigung entspricht \(\hat{\beta}_{i}\)) dargestellt. Die grüne Gerade repräsentiert die Modellierung des Zusammenhangs durch sogenannte Splines. Sollte der Zusammenhang nicht linear sein, so können eventuell die im weiteren vorgestellten Transformationen dazu benutzt werden, den Zusammenhang zu linearisieren.
Unabhängigkeit und Homoskedastizität
Weiterhin wird vorausgesetzt, dass die Residuen unabhängig sind und eine konstante Varianz aufweisen (\( V(\epsilon_{i}) = \sigma^{2}\)," Homoskedastizität"). Dies kann grafisch überprüft werden, indem die geschätzten Werte der abhängigen Variablen in einem Streudiagramm gegen die geschätzten Residuen des Models abgetragen werden (sog. Residuenplot). Die Annahmen des Regressionsmodells beziehen sich zwar auf die echten Residuen, diese können aber nicht beobachtet werden, da dazu das Wissen über die wahren Werte der Koeffizienten notwendig wäre. Es werden die geschätzten Werte der abhängigen Variable verwendet, da die echten Werte im linearen Regressionsmodell nicht unkorreliert mit den geschätzten Residuen sind. Desweiteren verstoßen die geschätzten Residuen auf Grund ihrer Berechnung gegen die Homoskedastizitätsannahme auch wenn keine Annahmenverletzung vorliegt. Deshalb werden die in Residuenplots immer die standardisierten Residuen (\(r_{i}=\frac{\hat{\epsilon}_{i}}{\hat{\sigma}\sqrt{1-h_{ii}}}\), folgend aus der Schreibweise: \(\hat{\epsilon}=(I-H)y=y-X(X'X)^{-1}X'y\)) gegen die geschätzten Werte der unabhängigen Variable geplottet.
Die Punkte in dem Diagramm sollten unsystematisch streuen. Das Auftreten einer Trichterform deutet auf eine Verletzung der Annahme konstanter Varianzen („Heteroskedastizität“) hin. Ist eine Systematik in den Punkten erkennbar, so ist diese meist auf eine Verletzung der Unabhängigkeitsannahme zurückzuführen. In Dem Fall (A) verteilen sich die Residuen ungefähr in einem gleichbleibend dickem horizontalen Band. Hier sind weder Abhängigkeiten, noch Heteroskedastizität erkennbar. Auf den Streudiagrammen (B,C,F) sind "Trichter" oder "Rauten" erkennbar. Das weist also auf die Verletzung der Homoskedastizitätsannahme hin und könnte mit dem Goldfeld-Quandt-Test weiter untersucht werden. Fälle wie (D) und (E) zeigen einen quadratischen/ logarithmischen Zusammenhang. Die Residuen streuen also nicht zufällig, sondern es ist eine klare Systematik erkennbar. Oft hängt diese Annahmenverletzung mit Problemen der Nichtlinearität (zwischen abhängiger und unabhängiger Variable) zusammen.
Beobachtungen mit großem Einfluss auf die Parameterschätzer lassen sich ebenso in dieser Art von Streudiagramm identifizieren.
Normalverteilungsannahme
Damit den F-Test und die t-Tests für die Parameter sinnvoll interpretiert weden können, müssen die Residuen normalverteilt sein. Um dies grafisch zu prüfen, kann ein Histogramm der standardisierten Residuen verwendet werden. Das Histogramm wird oft zusammen mit der Dichte der Standardnormalverteilung dargestellt. Die Form des Histogramms sollte möglichst der der Kurve entsprechen. Das vorliegende Histogramm zeigt, dass die Verteilung der Residuen im Vergleich zur Normalverteilung eher rechtsschief ist.
Eine weitere Möglichkeit zur Überprüfung der Normalverteilungsannahme der geschätzten Residuen sind Quantil-Quantil (Q-Q) Plots. Hierbei werden die Quantile der Fehlerterme gegen die theoretischen Quantile der Standardnormalverteilung abgetragen. Dieser Q-Q Plot weißt auf starke Abweichungen zwischen den Verteilungen hin. Die Punkte der hohen Quantile liegen über der eingezeichneten Geraden. Liegen alle Punkte auf der Geraden, sind die Verteilungen identisch. Der vorliegende Q-Q Plot spricht für eine linksschiefe Verteilung (positive Schiefe). Neben der graphischen Annahmenprüfung können auch Tests auf Normalverteilung wie der Shapiro-Wilk-Test oder der Kolmogorow-Smirnov-Test durchgeführt werden. Falls die Normalverteilungsannahme nicht erfüllt sein sollte, gibt es die Möglichkeit Variablentransformationen durchzuführen. Ein klassisches Transformationsbeispiel ist die Variable Einkommen. Dieses ist häufig nicht normalverteilt, das durch Logarithmierung transformierte Einkommen jedoch meist schon.
Graph (A) kann als "idealer" Q-Q Plot gesehen werden, wobei die Punkte sehr nahe an oder sogar auf der Gerade liegen. Im Fall (B) hat die Verteilung der Residuen dickeren Enden als die Normalverteilung. Der Graph (C) zeigt das typische Verhalten einer Verteilung mit dünneren Enden als bei einer Normalverteilung (S-Grafik). Grafiken (D) und (E) zeigen im Vergleich Muster, mit rechtsschiefer und linksschiefer Verteilung.
.