Ursache für die Annahmeverletzung
Die Annahme verlangt, dass die Residuen nicht miteinander korrelieren, das heißt: \(cov(\epsilon_i, \epsilon _j)=0\) für alle \(i \neq j\). Die Annahmeverletzung \(cov(\epsilon_i, \epsilon _j)\neq0\) führt zur nicht diagonalen Kovarianzmatrix: \(cov(\epsilon_i, \epsilon _j)=\sigma^2\Omega\), wobei \(\Omega\) eine nicht-diagonale Matrix ist. Die Annahme ist insbesondere für Zeitreihendaten relevant, da eine zeitliche Systematik in den Residuen vorhanden sein kann.
Bei Querschnittsdaten wird die Unkorreliertheit der Residuen aus der zufälligen Stichprobenziehung hergeleitet. Wenn die gezogenen Beobachtungen zufällig ausgewählt sind, sind auch die unbeobachtbaren Faktoren, die sich in den Residuen niederschlagen, zufällig verteilt und nicht miteinander korreliert.
Korrelation der Residuen kann aus folgenden Gründen auftreten:
- Nicht-Berücksichtigung relevanter Regressoren
- Autokorrelation in Zeitreihendaten
Überprüfung der unabhängigen Störgrößen und Konsequenz der Annahmeverletzung
Mithilfe des Box-Pierce und Ljung-Box-Tests können mehrere Autokorrelationskoeffizienten darauf getestet werden, ob sie sich signifikant von null unterscheiden. Die Nullhypothese lautet \(H_0: \rho_1(\epsilon _i)=\rho_2(\epsilon _i)=...=\rho_L(\epsilon i)=0\), die Gegenhypothese \(H_1: \rho_l \neq 0\) gilt für mindestens ein \(l\), wobei \(\rho_l(\epsilon_i)\): der Korrelationskoeffizient der Residuen zum Lag \(l\) und \(L\): die Anzahl der zu testenden Autokorrelationen.
Teststatistik nach Box/Pierce: \(Q_{BP}=N{\Sigma}_{l=1}^K \hat{\rho_l}^2 \sim \chi_L^2\)
Teststatistik nach Ljung/Box: \(Q_{K}=N(N+2){\Sigma}_{l=1}^K \frac{\hat{\rho_l}^2}{T-K} \sim \chi_L^2\)
wobei \(N\): Stichprobengröße, \(K\): Anzahl der Regressoren, \(\chi_L^2\): Chi-Quadrat-Verteilung mit \(L\) Freiheitsgraden und \(T\): Anzahl der Beobachtungen.
Wenn die Teststatistik größer als der kritische Wert aus der Chi-Quadrat-Verteilung mit \(L\) Freiheitsgraden ist, kann die \(H_0\) verworfen werden.
Andere Tests, die die Autokorrelation der Störgröße überprüfen, sind z.B.: Breusch-Godfrey-Test und Durbin-Watson-Test (Heij et al. 2004).
Wenn die Annahme der unabhängigen Residuen verletzt ist, sind die KQ-Schätzer noch unverzerrt aber nicht mehr BLUE. Das heißt, die Standardabweichungen der KQ-Schätzer sind nicht korrekt. Somit sind das Konfidenzintervall und die Hypothesentests basierend auf den Standardabweichungen auch nicht korrekt.
Beispiel 9: Autokorrelation bei Zeitreihendaten |
|---|
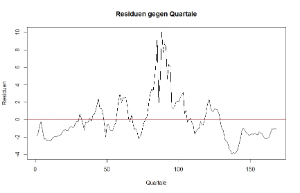
Der Plot zeigt die Residuen einer Regression des Zinssatzes von Staatsanleihen auf den Pfund/Dollar-Wechselkurs. Man sieht, dass die Residuen klare Autokorrelation aufweisen. Auf positive Residuen folgen eher positive und auf negative Residuen folgen negative. Die Kovarianz der Residuen ist somit keine diagonale Matrix. Ein Box-Pierce-Test verwirft die Nullhypothese: "Keine Autokorrelation" sehr deutlich.
|
Korrektur der Annahmeverletzung
Die Autokorrelation kann auftreten, wenn eine relevante unabhängige Variable nicht in das Regressionsmodell aufgenommen wird. In diesem Fall wird der Effekt der relevanten Variable in den Residuen beobachtet. Somit können die Residuen korrelieren. Wenn die relevante unabhängige Variable aufgenommen wird, verschwindet die Korrelation der Residuen. (Chatterjee / Hadi 2006)
Alternative
Alternative 1: HAC (Heteroscedasticity and Autocorrelation Consistent) Standardabweichungen (Newey-West Standardabweichungen)
Da die KQ-Schätzer trotz der Annahmeverletzung noch unverzerrt sind, kann man die Schätzer weiter benutzen und für das Konfidenzintervall und die Hypothesentests robuste Standardabweichungen des Schätzers benutzen. Newey-West Schätzer schätzen eine Heteroskedastizität- und Autokorrelation-konsistente Kovarianzmatrix der Parameter.
Alternative 2: Verallgemeinerte Kleinste-Quadrate-Schätzung (englisch GLS: Generalized Least Squares): AR (1) (Autoregressiv erster Ordnung)
GLS setzt voraus, dass die Störgröße autoregressiv erster Ordnung ist: \(\epsilon_i=\rho\epsilon_{i-1}+\upsilon_i\) wobei \(|\rho|<1\) und \(\upsilon_i\): unkorrelierte zufällige Störgröße mit \(E(\upsilon_i)=0\) und \(Var(\upsilon_i)=\sigma^2_{\upsilon}\). Das Model mit autoregressiven Störgrößen kann mit \(\rho y_{i-1}= \rho \beta_0 + \rho \beta _{1}x_{1, i-1} + ... + \rho \beta _{K-1}x_{K-1, i-1} + \rho\epsilon_{i-1}\) wie folgt transformiert werden:
\[y_i - \rho y_{i-1}= \beta_0 (1-\rho) + \beta_{1} (x_{1, i} - x_{1, i-1}) + ... + \beta_{K-1} (x_{K-1, i}x_{K-1, i-1}) +\upsilon_i\].
Die Gleichung kann umgeschrieben werden:
\[y^{\ast}_i=\beta_0 x^{\ast}_{0, i} + \beta_1 x^{\ast}_{1, i}+...+\upsilon_i\]
Das transformierte Modell hat keine korrelierte Störgröße und die Schätzer können durch die KQ-Schätzung effizient geschätzt werden.
Code R
Code Stata
Code SPSS
Code SAS
Daten als CSV-Datei
BLUE (Best linear unbiased estimator)
Unter den aufgeführten Annahmen 1-5 ist der Kleinst-Quadrate Schätzer der beste (d.h. mit der geringsten Varianz) lineare, unverzerrte Schätzer. Diese Eigenschaft des Kleinst-Quadrate Schätzers werden im Satz von Gauß-Markov bewiesen.
Bildergalerie
|
|
|
|
