- Erstellt von Ann-Kristin Kreutzmann, zuletzt aktualisiert von Anonym vor etwa 2 Stunden Lesedauer: 11 Minute(n)
In vielen Fragestellungen ist der Zusammenhang zwischen zwei Variablen X und Y oder mehreren Variablen, z.B. X1, X2 und Y von Interesse, wie z.B.
- steigt der Konsum von Speiseeis mit der Temperatur
- haben Männer ein höheres Einkommen als Frauen oder
- ist das Einkommen höher mit besserer Bildung und mehr Berufserfahrung
Diese Zusammenhänge können anhand von Funktionen beschrieben werden, die unterschiedliche Formen annehmen können. Die einfachste Form ist der lineare Zusammenhang. Dabei erklärt die Variable X oder mehrere Variablen die Eigenschaften der abhängigen Variable Y. Im Folgenden soll darauf eingegangen werden, wie man die Form der Funktion erkennt und wie man im Falle eines linearen Zusammenhangs diesen adäquat beschreiben kann. Dabei werden Lösungswege in den vier Statistikprogrammen R, SAS, SPSS und Stata zur Verfügung gestellt. Die lineare Regression wird hier beispielhaft erläutert, sodass für eine theoretischere Einführung auf Kapitel 19 aus dem Buch Einführung in die Statistik: Analyse und Modellierung von Daten von Rainer Schlittgen sowie Wikipedia - Lineare Regression verwiesen wird. Eine hilfreiche Einführung wird auch von der Pennsylvania State University angeboten.
Inhaltsverzeichnis
fu:stat bietet regelmäßig Schulungen für Hochschulangehörige sowie für Unternehmen und weitere Institutionen an. Die Inhalte reichen von Statistikgrundlagen (Deskriptive, Testen, Schätzen, lineare Regression) bis zu Methoden für Big Data. Es werden außerdem Kurse zu verschiedenen Software-Paketen gegeben.
Variablen und deren Zusammenhang
Auch wenn es plausibel erscheint, dass der Zusammenhang zwischen zwei Variablen linear ist, geht jeder Regression voraus, den Zusammenhang aus den gegebenen Daten zu erkennen. Dafür ist auch das Skalenniveau der Variablen relevant, um eine sinnvolle Abbildung zu bekommen. Bei einer Regression, in der eine Variable X eine Variable Y erklärt, gibt es die Möglichkeiten, dass X metrisch oder kategorial ist ebenso wie Y metrisch oder kategorial sein kann.
Für das erste Beispiel sind sowohl die erklärende Variable X, als auch die abhängige Variable Y metrisch.
Einführung in das Bespiel: Körpergewicht und Körpergröße Die Variablen, anhand derer hier der Zusammenhang zweier metrischer Variablen erklärt werden soll, sind das Körpergewicht und die Körpergröße. Die Variablen entstammen dem Datensatz Umfragedaten_v1_an. Das Körpergewicht wird in kg und die Körpergröße in cm gemessen. Meistens unterliegt einer statistischen Fragestellung eine theoretische Hypothese. In diesem Beispiel soll folgende Hypothese überprüft werden: Hypothese: Das Körpergewicht steigt mit zunehmender Körpergröße. |
|---|
Für einen ersten Überblick über die beiden Variablen bieten sich für das entsprechende Skalenniveau passende Maße an. Bei metrischen Variablen können dies z.B. der Mittelwert oder der Median sowie das Minimum und das Maximum sein. In diesem Beispiel liegt das durchschnittliche Körpergewicht bei ca. 78kg und die Körpergröße im Schnitt bei ca. 172cm (siehe Abschnitt 1 in den Beispielcodes).
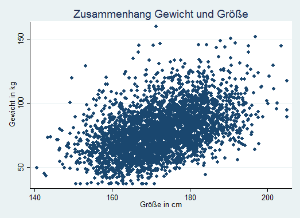
Zur Überprüfung der Hypothese reichen jedoch keine Informationen über die einzelnen Variablen, sondern es soll ein Zusammenhang zwischen diesen beiden herausgestellt werden. Eine einfache Methode ist, die Variablen in einem Streudiagramm darzustellen, in denen jeweils eine Kovariate gegen die abhängige Variable abgebildet wird. Da hier das Körpergewicht mit Hilfe der Körpergröße erklärt werden soll, wird das Körpergewicht auf der Y-Achse und die Körpergröße auf der X-Achse abgebildet (siehe Abschnitt 2.1. in den Beispielcodes).
Streudiagramme


Anhand der Streudiagramme kann man erkennen, dass für den Zusammenhang zwischen Körpergewicht und Körpergröße eine lineare Funktion angenommen werden kann.
Streudiagramm
Diese Streudiagramme bilden die Wertepaare (GRO,GEW) des Datensatzes Umfragedaten ab. Das rechte Streudiagramm berücksichtigt im Vergleich zum linken Streudiagramm, dass einige Wertepaare häufiger Vorkommen als andere. Beide Streudiagramme wurden erstellt mit der Software Stata.
Interpretation einer linearen Regression
Im Folgenden werden einzelne Begriffe, die bei der Auswertung einer linearen Regression auftauchen, kurz beschrieben. Dies ist eine ungeordnete Ansammlung an Komponenten, die in den Outputs der unterschiedlichen Statistikprogramme vorkommen. Im nächsten Abschnitt wird die Liste an den vorliegenden Output je nach Programm angepasst. Alle Zahlen, die in Beispielen genutzt werden, sind in den Outputs der verschiedenen Statistikprogramme zu finden.
Komponenten und Begriffe
\(x_i\) : unabhängige Variable
\(y_i\) : abhängige Variable
Formulierung eines einfachen linearen Modells: \(y_{i}= \beta_0 + \beta _{1}x_i\)
Bei Gültigkeit dieser strikten Beziehung müssten alle Beobachtungen im Streudiagramm auf einer Geraden mit dem Achsenabschnitt \(\beta_0\) und der Steigung \(\beta_1\) liegen.
Für die Praxis muss das Modell erweitert werden. Der zusätzliche Term \(\epsilon_i\) beschreibt die Abweichung (Fehler) der abhängigen Variable von der Geraden: \(y_{i}= \beta_0 + \beta _{1}x_i + \epsilon_i\)
Hier soll der Zusammenhang zwischen Körpergröße in cm und dem Körpergewicht in kg erklärt werden: Modell: \(GEW_i = \beta_0 + \beta_1 \cdot GRO_i + \epsilon_i\) |
|---|
Das multiple lineare Regressionsmodell in seiner allgemeinen Form mit \(P\) Kovariaten wird folgendermaßen beschrieben:
\[ Y_{i} = \beta_0 + \beta_1 \cdot x_{i,1} + \beta_2 \cdot x_{i,2} + \ldots + \beta_P \cdot x_{i,P} + \epsilon_i \qquad (i=1,\ldots ,n) \]
Die Güte des Modells
1. Gesamtzahl an Beobachtungen:
Die gesamte Anzahl an Beobachtungen im Datensatz entspricht der Anzahl an Zeilen. Diese wird häufig mit n gekennzeichnet. Im Umfragedatensatz gibt es insgesamt 3471 Beobachtungen.
2. Gelöschte Beobachtungen:
Bei fehlenden Werten in Variablen können Beobachtungen für die Modellanalyse nicht berücksichtigt werden. Im Beispiel sind dies 47 Beobachtungen.
3. Zahl der Beobachtungen:
Hiermit ist die Zahl der Beobachtungen gemeint, die zur Anpassung des Modells genutzt wird. Das bedeutet, dass diese Anzahl sich aus der Differenz der Gesamtzahl an Beobachtungen und den gelöschten Beobachtungen auf Grund von fehlenden Werten in den gewünschten Variablen ergibt. In dem Modell wurden 3424 Beobachtungen genutzt.
4. Der empirische F-Wert
Der F-Wert dient zur Überprüfung der Gesamtsignifikanz des Modells. Die F-Statisik gibt den Anteil der erklärten Varianz an der unerklärten Varianz an. Dabei sind die Freiheitsgrade (siehe Anova-Block) zu berücksichtigen, die sich aus der Anzahl der Beobachtungen und der Parameter berechnet. Hier ist jedoch zu beachten, dass mit n die Zahl der Beobachtungen und mit P die Zahl der Einflußvariablen (Parameter) gemeint ist, die im Modell genutzt wurden.
$$F = \frac{MS(R)}{MS(F)} = \frac{\frac{SS(R)}{P}}{\frac{SS(F)}{(n −P −1)}} = \frac{\frac{SS(R)}{SS(G)}/P}{\frac{SS(F)}{SS(G)}/(n −P −1)} = \frac{\frac{R^{2}}{P}}{\frac{1-R^{2}}{(n −P −1)}} = \frac{R^{2}}{1-R^{2}} \frac{(n −P −1)}{P} $$
Berechnung der F-Statistik für das Beispiel Körpergewicht-Körpergröße: Die F-Statistik kann über zwei verschiedene Wege berechnet werden. Entweder nutzt man die Mean Squares (MS), bzw. die Sum of Squares (SS) oder das R-Quadrat. Hier sollen einmal beide Wege beispielhaft gezeigt werden.
|
|---|
5. p-Wert zur F-Statistik:
Die Nullhypothese des F-Tests besagt, dass alle Koeffizienten gleich 0 sind. Hingegen ist die Alternative, dass mindestens ein Koeffizient ungleich 0 ist – es also mindestens eine Kovariate im Modell gibt, die signifikanten Einfluss auf die abhängige Variable ausübt. Die Nullhypothese wird abgelehnt, wenn der p-Wert kleiner als ein gewähltes Signifikanzniveau ist.
Interpretation im Beispiel Körpergewicht-Körpergröße: Der p-Wert für das Regressionsmodell liegt bei 0.0000 und ist somit kleiner als ein Signifikanzniveau von α = 0.05. Daher kann die Nullhypothese des F-Tests, dass alle Koeffizienten gemeinsam gleich 0 sind, abgelehnt werden. |
|---|
6. Empirisches Bestimmtheitsmaß R²
Das R² basiert auf dem Varianzzerlegungssatz, der besagt, dass sich die Varianz der abhängigen Variablen als die Summe eines Varianzteils, der durch das Regressionsmodell erklärt wird, und der Varianz der Residuen (nicht erklärte Varianz) schreiben lässt. Das Bestimmtheitsmaß ist der Quotient aus erklärter Varianz und Gesamtvarianz. Als Anteilswert kann das R² Werte zwischen 0 und 1 annehmen.
\( R^{2} = \frac{SS(R)}{SS(G)} = \frac{\sum_{i=1}^{n} (\hat{y}_{i} - \bar{y})^{2}}{\sum_{i=1}^{n} (y_{i} - \bar{y})^{2}} = 1 - \frac{\sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2}}{\sum_{i=1}^{n} (y_{i} - \bar{y})^{2}}\)
Berechnung und Interpretation des Bestimmtheitsmaßes für das Beispiel Körpergewicht-Körpergröße: $$R^{2} = \frac{259550.211}{945587.301} = 1- \frac{686037.09}{945587.301} = 0.2745$$ Ein \(R^{2}\) von 0.2745 bedeutet, dass 27.45% der Varianz in Gewicht durch das Modell erklärt werden können. |
|---|
Die Einschätzung der Höhe des Bestimmtheitsmaßes hängt oft vom Anwendungsfeld ab. Zur Beurteilung des eigenen Modells ist daher der Vergleich mit anderen Studien (im gleichen Feld) unerlässlich.
7. Korrigiertes R²
Durch das Hinzufügen einer neuen Kovariate in das Regressionsmodell kann sich das R² nie verschlechtern. Um das inflationäre Ergänzen von nutzlosen Variablen zu sanktionieren, gibt es das sog. „korrigierte R² “. Dies zieht für jede Kovariate im Modell einen „Strafterm“ ab und wächst somit nur an, wenn Kovariaten ergänzt werden, die das Modell deutlich verbessern.
$$R^{2} = 1 - \frac{\frac{1}{n-P-1} \sum_{i=1}^{n} (y_{i} - \hat{y}_{i})^{2}}{\frac{1}{n-1} \sum_{i=1}^{n} (y_{i} - \bar{y})^{2}}$$
Berechnung des korrigierten Bestimmtheitsmaßes für das Beispiel Körpergewicht-Körpergröße: $$R^{2} = 1 - \frac{\frac{1}{3424-1-1} 686037.09}{\frac{1}{3424-1} 945587.301} = 0.2743$$ Dieses \(R^{2}\) gibt nicht mehr den prozentualen Anteil an erklärter Varianz an, aber es gilt: Je höher das korrigierte \(R^{2}\), desto besser passt das Modell auf die Daten. |
|---|
8. Standardfehler des Schätzers:
Dieser entspricht der Wurzel der mittleren Abweichungsquadrate des Modells aus dem Anova-Block und beschreibt die Standardabweichung der Beobachtungen von den Prognosewerten:
\(\sqrt{MS(F)}\)
Schätzergebnisse
9. Abhängige oder endogene Variable:
Im Beispiel ist das Körpergewicht (GEW) die abhängige Variable.
10. Erklärende oder exogene Variable:
Im Beispiel ist die Körpergröße (GRO) die erklärende Variable.
11. Geschätzte Parameter:
Bei einer linearen Einfachregression gibt es zwei geschätzte Parameter \( \beta_0\) für den Achsenabschnitt und \( \beta_1\) für die Steigung. Der Parameter \( \beta_0\) gibt den geschätzten Wert der abhängigen Variablen an, wenn alle Kovariaten gleich 0 sind, was am Schnittpunkt mit der y-Achse der Fall ist. Der Steigungsparameter gibt an, wie stark die erklärende Variable (Körpergewicht) die abhängige Variable (Körpergröße) beeinflusst.
Schätzung im Beispiel Körpergewicht-Körpergröße: \(\hat{GEW}_i = -82.5748 + 0.9321 \cdot GRO_{i}\) Interpretation der Parameter: Der Parameter für die Konstante entspricht -82.5748. Das bedeutet, dass bei einer Körpergröße von 0 cm das geschätzte Körpergewicht bei ca. -82 kg liegen würde. Diese Interpretation ist natürlich sinnlos, weil eine Körpergröße von 0 cm unplausibel ist. Dem Überblick über die Variable Körpergröße kann man entnehmen, dass die kleinste Person eine Körpergröße von 143 cm angegeben hat. Der Steigungsparameter entspricht 0.9321. Das bedeutet, dass pro cm das Gewicht um ca. 0,93 kg steigt. |
|---|
12. Standardabweichung der Schätzung (Standardfehler, \(\hat{SF_{\beta_p}}\)):
Da die Parameter basierend auf einer Zufallsstichprobe geschätzt werden, unterliegen diese Schätzungen einer gewissen Ungenauigkeit, die durch die Standardabweichung der Schätzung quantifiziert wird. Standardfehler werden genutzt, um statistische Signifikanz zu überprüfen und um Konfidenzintervalle zu bilden.
13. T-Statistik (empirischer T-Wert).
Mit Hilfe eines t-Tests lässt sich prüfen, ob die Nullhypothese, dass ein Koeffizient gleich 0 ist, abgelehnt werden kann. Wenn dies nicht der Fall sein sollte, ist davon auszugehen, dass die zugehörige Kovariate keinen signifikanten Einfluss auf die abhängige Variable ausübt, d.h. die erklärende Variable ist nicht sinnvoll, um die Eigenschaften der abhängigen Variablen zu erklären.
Hypothese: \(H: \beta_p=0\) gegen \(A: \beta_p \neq 0\) mit \(p=0,1\)
Teststatistik: \(T_p = \frac{\hat{\beta_p}-0}{\hat{SF_{\beta_p}}}\) mit \(p=0,1\)
Verteilung unter H: \(T_p \sim t_{n-(P+1)}\) mit \(p=0,1\)
Testentscheidung (H ablehnen wenn): \(|T_p| > t_{n-(P+1), 1-\frac{\alpha}{2}}\) mit with \(p=0,1\)
Überprüfung, ob Körpergröße Einfluss auf das Körpergewicht hat, anhand der T-Statistik: Die Teststatistik vom Parameter für die Körpergröße ist \(T_1 = \frac{0.932}{0.0259} = 35.98\). Diese Teststatistik wird mit dem kritischen Wert verglichen ( \( \alpha = 0.05\)): \(|T_1| = 35,98 > 1,961 = t_{3424-(1+1), 1-\frac{\alpha}{2}}\). Schon anhand der Teststatistik kann man erkennen, dass die Nullhypothese \(\beta_1=0\) hier abgelehnt werden kann, d.h. dass die Körpergröße einen signifikanten Einfluss auf das Körpergewicht hat. |
|---|
14. p-Wert zur T-Statistik:
Zusätzlich zur T-Statisik wird meistens ein p-Wert ausgegeben. Aus einer methodisch-praktisch orientierten Perspektive gibt der p-Wert das kleinste Signifikanzniveau an, zu dem die Nullhypothese \(\beta_p=0\) gerade noch abgelehnt werden kann. Ist also das tatsächliche Signifikanzniveau \( \alpha \), welches vor dem Test gewählt wird, geringer als der p-Wert, so kann die Nullhypothese nicht abgelehnt werden.
Überprüfung, ob Körpergröße Einfluss auf das Körpergewicht hat, anhand des p-Wertes: Im Beispiel liegt der p-Wert zur Nullhypothese \(\beta_1=0\) unter 0,0001. Daraus kann man schließen, dass die Körpergröße einen signifikanten Einfluss auf das Körpergewicht ausübt. |
|---|
Der p-Wert gibt die Wahrscheinlichkeit an, dass wir unter der Nullhypothese einen Wert der Teststatistik beobachten, der noch stärker in Richtung Ablehnung der Nullhypothese geht. Das heißt, er macht eine Aussage über die Wahrscheinlichkeit der Beobachtung der Stichprobe, nicht aber direkt über die Wahrscheinlichkeit der Nullhypothese selbst.
Zum p-Wert gibt es viele Missverständnisse, selbst in veröffentlichter Literatur. Aussagen wie z.B. dass "der p-Wert den Fehler 1. Art wieder gibt" bzw. "die Wahrscheinlichkeit ist, dass unsere Hypothese wahr ist, gegeben, dass der Test abgelehnt wird", sind falsch und sollten in Arbeiten vermieden werden. Einige dieser Schwierigkeiten und Missverständnisse werden in dem folgenden Video angesprochen: Link zum Video.
Eine gute Quelle für die den richtigen Umgang und ein tieferes Verständnis vom p-Wert gibt es beispielsweise hier.
15. 95%-Konfidenzintervall:
Konfidenzintervalle sind im Allgemeinen eine Möglichkeit, die Genauigkeit der Schätzung zu überprüfen. Ein 95%-Konfidenzintervall ist der Bereich, der im Durchschnitt in 95 von 100 Fällen den tatsächlichen Wert des Parameters einschließt.
Konfidenzintervall für den Steigungsparameter in der Beispielregression: [0.932062 - 1.96 * 0.0259041; 0.932062 - 1.96 * 0.0259041] = [0.881273; 0.982851] |
|---|
Anova-Block
16. Modell-Quadratsumme/Regressions-Quadratsumme (SS(R)):
Mit SS(R) wird die Varianz der abhängigen Variablen angegeben, die durch das Modell bzw. durch die Regression erklärt werden kann. $$\sum_{i=1}^{n} (\hat{y}_{i} - \bar{y})^{2}$$
17. Residuen-Quadratsumme (SS(F)):
Die Varianz, die nicht durch das Modell bzw. die Regression erklärt werden kann, wird mit SS(F) beschrieben. $$\sum_{i=1}^{n} (y_{i} - \hat{y}_{i} )^{2}$$
18. Gesamtstreuung (Gesamt-Quadratsumme):
Die Varianz der abhängigen Variable lässt sich als Summe der durch das Modell erklärten Varianz und der unerklärten Varianz darstellen: erklärte Abweichung + unerklärte Abweichung (SS(G)= SS(R) + SS(F)).
Gesamtstreuung und die einzelnen Komponenten im Beispiel Körpergewicht-Körpergröße: SS(G) = SS(R) + SS(F) = 259550.211 + 686038.09 = 945587.301 |
|---|
19. Freiheitsgrade (FG):
Freiheitsgrade gesamt: n - 1
Freiheitsgrade der Regression: 1
Freiheitsgrade der Residuen: FGGesamt - 1
20. Mittlere Abweichungsquadrate:
Mittlere Abweichungsquadrate sind die Quotienten aus Quadratsumme und Freiheitsgraden.
Mittleres Abweichungsquadrat der Regression: MS(R) = SS(R)/DF(R)
Mittleres Abweichungsquadrat der Residuen: MS(F) = SS(F)/DF(F)
Mittleres Abweichungsquadrat gesamt: MS(G) = SS(G)/DF(G)
Outputs in den verschiedenen Statistikprogrammen
Die Outputs einer linearen Regression unterscheiden sich teils in den verschiedenen Statistikprogrammen. Sowohl sind die Werte unterschiedlich angeordet, als auch werden teils nicht die gleichen Werte ausgegeben.
Im Folgenden werden die Werte 1-20, wenn vorhanden, an den Output der verschiedenen Statistikprogramme geschrieben, damit die Werte im Output gefunden werden können.
Modellannahmen und deren Überprüfung
Eine lineare Regression unterliegt unterschiedlichen Annahmen. Diese betreffen vor allem die Fehlerterme, auch Residuen genannt. Auf den folgenden Unterseiten werden die Annahmen genannt und Wege aufgeführt, wie diese überprüft werden können. Einen ausführlicheren Überblick von Annahmen und deren Konsequenzen bietet auch eine Zusammenfassung der TU Dresden.
Annahme 2: Unabhängigkeit zwischen Regressoren und Residuen
Annahme 3: Homoskedastische Residuen \(Var(\epsilon_i)=\sigma^2\) mit Erwartungswert \(E(\epsilon_i) = 0\)
Annahme 4: Unabhängigkeit der Residuen
Interaktive Minianwendung
In diesem kleinen Applet kann man sich die Regressionsgerade, geschätzte Residuen, quadrierte geschätzte Residuen, den Korrelationskoeffizienten und das Bestimmtheitsmaß anzeigen lassen.
Ergänzen Sie einen Wert von x = 22 und y = 78. Was passiert mit der Modellgüte und der Parameterschätzung?
Bildergalerie

|

|
|

|
Literatur
Chatterjee, Samprit und Ali S. Hadi 2006. Regression analysis by example. Hoboken: Wiley.
Heij, Christian, de Boer, Paul, Franses, Philip Hans, Teun Kloek und Herman K. van Dijk. 2004. Econometric Methods with Applications in Business and Economics. Oxford: Oxford University Press.
Hill, Rufus Carter, William E. Griffiths und Guay C. Lim. 2012. Principles of econometrics. Hoboken: Wiley.
Hübler, Olaf. 2005. Einführung in die empirische Wirtschaftsforschung. München: Oldenbourg.
Ohr, Dieter. 2010. "Lineare Regression: Modellannahmen und Regressionsdiagnostik" in: Wolf, Christof und Henning Best (Hrsg.). Handbuch der sozialwissenschaftlichen Datenanalyse. Wiesbaden: VS Verlag für Sozialwissenschaften, 639-675.
Schlittgen, Rainer. 2009. Multivariate Statistik. München: Oldenbourg.
Schlittgen, Rainer. 2013. Regressionsanalysen mit R. München: Oldenbourg.
von Auer, Ludwig. 2016. Ökonometrie Eine Einführung. Berlin, Heidelberg: Springer Gabler.
Wooldridge, Jeffrey M. 2013. Introductory econometrics : a modern approach. South-Western Cengage Learning: Mason, Ohio u.a.
- Keine Stichwörter
